题目内容
满足不等式x2-x<0的x的取值范围是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:解不等式x2-x<0,即可得出x的取值范围.
解答:
解:不等式x2-x<0可化为
x(x-1)<0,
解得0<x<1;
∴x的取值范围是(0,1).
故答案为:(0,1).
x(x-1)<0,
解得0<x<1;
∴x的取值范围是(0,1).
故答案为:(0,1).
点评:本题考查了求一元二次不等式的解集问题,解题时应按照解一元二次不等式的步骤解答即可,是容易题.

练习册系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| B、若命题p:?x∈R,x2+x+1=0,则“?p”为:?x∈R,x2+x+1≠0 |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、若“p∧q”为假命题,则p,q均为假命题 |
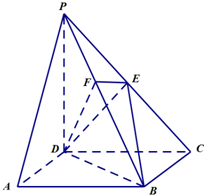 如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.
如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.