Question

当k＞0时，两直线kx-y=0，2x+ky-2=0与x轴围成的三角形面积的最大值为

 

．

Answer 1

考点：简单线性规划

专题：数形结合

分析：作出两直线与x轴围成的三角形，求出B的坐标，写出三角形面积公式，然后利用基本不等式求最值．

解答： 解：由两直线kx-y=0，2x+ky-2=0与x轴围成的三角形如图，

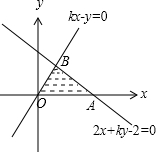
联立

kx-y=0 2x+ky-2=0

，解得B（

2

k2+2

，

2k

k2+2

）．
则S△OAB=

1

2

×1×

2k

k2+2

=

k

k2+2

=

1

k+ 2 k

≤

1

2 k• 2 k

=

2

4

．
当且仅当k=

2

k

，即k=

2

时上式取等号．
故答案为：

2

4

．

点评：本题考查线性规划问题，近年来线性规划问题是高考数学考试的热点，数形结合是数学思想的重要手段之一，是连接代数和几何的重要方法．随着要求数学知识从书本到实际生活的呼声不断升高，线性规划这一类新型数学应用问题要引起重视，是中档题．