题目内容
几何体的三视图如图所示：
其中正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，则该几何体的全面积为 ．
其中正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，则该几何体的全面积为
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由几何体的三视图可得几何体是正四棱台，连接BD，B′D′，过B′分别作下底面及BC的垂线交BD于E，BC于F，根据正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，可得A′B′′=3，AB=9，棱台的高为B′E=4，求出正四棱台的斜高与正四棱台的高，进而根据有关的公式求出几何体的全面积．
解答：
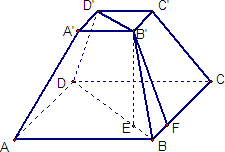解：∵正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，
∴A′B′=3，AB=9，棱台的高为B′E=4，
∴侧棱BB′=
=
，斜高B′F=
=5，
∴全面积S=32+92+4×
×5=210，
故答案为：210．
解：∵正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，∴A′B′=3，AB=9，棱台的高为B′E=4，
∴侧棱BB′=
| 18+16 |
| 34 |
| 34-9 |
∴全面积S=32+92+4×
| 3+9 |
| 2 |
故答案为：210．
点评：本题借助几何体的三视图考查几何体表面积D计算，考查了学生的空间想象能力与识图，用图能力．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
当a≠0时，函数y=ax+b和函数y=bax的图象可能是（ ）
A、 |
B、 |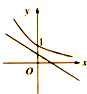
C、 |
D、 |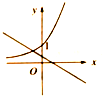
y=2sin（
x-
）的周期为（ ）
| 1 |
| 2 |
| π |
| 6 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
若函数f（x）满足f（x）=elnx+x2f（1）+x，则f（1）的值为（ ）
| A、-2e-1 | B、-e-1 |
| C、-1 | D、e+1 |
已知全集U={1，2，3，4}，集合A={1，2，4}，B={2，3}，则图中阴影部分表示的集合为（ ）| A、{2} |
| B、{3} |
| C、{1，4} |
| D、{1，2，3，4} |
在空间，下列命题中正确的是 （ ）
| A、没有公共点的两条直线平行 |
| B、与同一直线垂直的两条直线平行 |
| C、平行于同一直线的两条直线平行 |
| D、已知直线a不在平面α内，则直线a∥平面α |