题目内容
下面有5个命题:
①函数y=|sinx+
|的最小正周期是π.
②终边在y轴上的角的集合是{a|a=
,k∈Z}.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有3个公共点.
④把函数y=3sin(2x+
)的图象向右平移得到y=3sin2x的图象.
⑤函数y=sinx在[0,π]上是减函数.
其中,真命题的编号是 .(写出所有真命题的编号)
①函数y=|sinx+
| 1 |
| 2 |
②终边在y轴上的角的集合是{a|a=
| kπ |
| 2 |
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有3个公共点.
④把函数y=3sin(2x+
| π |
| 3 |
⑤函数y=sinx在[0,π]上是减函数.
其中,真命题的编号是
考点:命题的真假判断与应用,根的存在性及根的个数判断,函数y=Asin(ωx+φ)的图象变换
专题:综合题,简易逻辑
分析:利用三角函数的性质,逐个判断,即可得出结论.
解答:
解:①函数y=|sinx+
|的最小正周期是2π,故①不正确.
②终边在y轴上的角的集合是{a|a=kπ+
,k∈Z},故②不正确.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有1个公共点(0,0),故③不正确.
④把函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x的图象,故正确.
⑤函数y=sinx在[
,π]上是减函数,故不正确.
故答案为:④.
| 1 |
| 2 |
②终边在y轴上的角的集合是{a|a=kπ+
| π |
| 2 |
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有1个公共点(0,0),故③不正确.
④把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
⑤函数y=sinx在[
| π |
| 2 |
故答案为:④.
点评:本题考查命题的真假判断与应用,考查三角函数的性质,正确理解三角函数的性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合A={1,2,3,4},B⊆A,已知1∈B,且B中含有3个元素,则集合B有( )
A、
| ||
B、
| ||
C、
| ||
D、
|
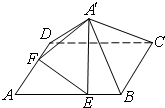 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2