题目内容
在数列{an}中，前n项和Sn=3n+p（p为常数），若{an}是以q为公比的等比数列，则p+q的值是（ ）
| A、0 | B、1 | C、2 | D、4 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：利用Sn=3n+p（p为常数），可得a1，a2，a3，再利用等比数列的定义即可得出．
解答：
解：∵Sn=3n+p（p为常数），
∴a1=S1=3+p，a2=S2-S1=32-31=6，a3=S3-S2=33-32=18．
∵{an}是以q为公比的等比数列，
∴q=
=
=3．
3=
=
，解得p=-1．
∴p+q=2．
故选：C．
∴a1=S1=3+p，a2=S2-S1=32-31=6，a3=S3-S2=33-32=18．
∵{an}是以q为公比的等比数列，
∴q=
| a3 |
| a2 |
| 18 |
| 6 |
3=
| a2 |
| a1 |
| 6 |
| 3+p |
∴p+q=2．
故选：C．
点评：本题考查了利用递推式求数列的通项公式、等比数列的定义，考查了推理能力和计算能力，属于基础题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如果f（x）=mx2+（m-1）x+1在区间（-∞，1]上为减函数，则m的取值范围（ ）
A、（0，
| ||
B、[0，
| ||
C、[0，
| ||
D、（0，
|
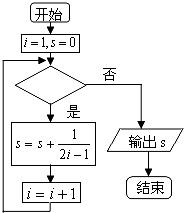如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |
| A、i≤1006 |
| B、i＞1006 |
| C、i≤1007 |
| D、i＞1007 |
图为一个半球挖去一个圆锥的几何体的三视图，则该几何体的表面积为（ ）
A、（
| ||||
B、（
| ||||
C、（4+2
| ||||
D、（8+4
|
函数y=x2-x，（-1＜x＜4）值域是（ ）
A、[-
| ||
| B、（2，12） | ||
| C、（2，20） | ||
D、[-
|
若f（cosx）=
，x∈[0，π]，则f（-
）等于（ ）
| x |
| 2 |
| 1 |
| 2 |
A、cos
| ||
B、
| ||
C、
| ||
D、
|
复数z满足
=1（i为虚数单位），则复数z为（ ）
| 1-zi |
| i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |