题目内容
设P点是曲线y=x3-
x+
上的任意一点,P点处切线倾斜角为α,则角α的取值范围是( )
| 3 |
| 2 |
| 3 |
A、[0,
| ||||
B、[0,
| ||||
C、[
| ||||
D、(
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:求出曲线解析式的导函数,根据完全平方式大于等于0求出导函数的最小值,由曲线在P点切线的斜率为导函数的值,且直线的斜率等于其倾斜角的正切值,从而得到tanα的范围,由α的范围,根据正切函数的值域得到自变量α的范围.
解答:
解:∵y′=3x2-
≥-
,∴tanα≥-
,
又∵0≤α≤π,
∴0≤α<
或
≤α<π.
则角α的取值范围是[0,
)∪[
,π).
故选A.
| 3 |
| 3 |
| 3 |
又∵0≤α≤π,
∴0≤α<
| π |
| 2 |
| 2π |
| 3 |
则角α的取值范围是[0,
| π |
| 2 |
| 2π |
| 3 |
故选A.
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用切线的斜率与倾斜角之间的关系k=tanα进行求解.

练习册系列答案
相关题目
若随机向一个边长为2的正三角形内丢一粒豆子,则豆子落在此三角形内切圆内的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知直线y=
x-12,则其倾斜角为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
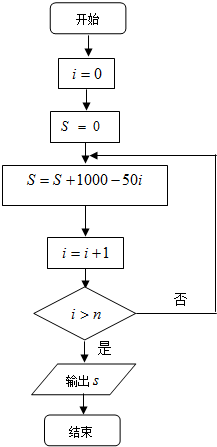 某企业生产的某种产品经市场调查得到如下信息,在不做广告宣传时月销售量为1000件;若做广告宣传,月销售量S件与广告费n千元(n∈N*)的关系可用右边流程图来表示:
某企业生产的某种产品经市场调查得到如下信息,在不做广告宣传时月销售量为1000件;若做广告宣传,月销售量S件与广告费n千元(n∈N*)的关系可用右边流程图来表示: