题目内容
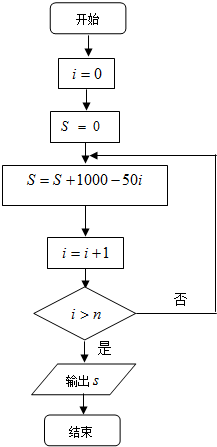 某企业生产的某种产品经市场调查得到如下信息,在不做广告宣传时月销售量为1000件;若做广告宣传,月销售量S件与广告费n千元(n∈N*)的关系可用右边流程图来表示:
某企业生产的某种产品经市场调查得到如下信息,在不做广告宣传时月销售量为1000件;若做广告宣传,月销售量S件与广告费n千元(n∈N*)的关系可用右边流程图来表示:(Ⅰ)根据流程图,试写出广告费n分别等于1千元和2千元时所对应的月销售量S的值;
(Ⅱ)试写出月销售量S与广告费n千元的函数关系式;
(Ⅲ)若销售一件产品获利10元,该企业做几千元广告时,才能月获利最多,最多是多少?
考点:程序框图
专题:算法和程序框图
分析:(1)分别求令n=1,n=2时相应的S的值即可;
(2)根据程序框图,直接求解即可;
(3)结合(2)直接求解.
(2)根据程序框图,直接求解即可;
(3)结合(2)直接求解.
解答:
解:(1)当n=1时,
S=1000+1000-50×1=2×1000-50×1=1950.
当n=2时,S=3×1000-50×(1+2)=2850.
(2)依题意,
S=(n+1)•1000-50•(1+2+3+…+n)
=(n+1)•1000-50•
,
=-25n2+975n+1000,n∈N*.
(3)依题意,当月销售量S最大时,可获得最大利润.
由(2)知S=-25n2+975n+1000=-25(n2-39n)+1000.
从企业利益考虑,当n=19时,即该企业的广告费为19000元时,
月销售量S的最大值等于(19+1)×1000-50×=10500件,
此时月利润的最大值为105000元.
S=1000+1000-50×1=2×1000-50×1=1950.
当n=2时,S=3×1000-50×(1+2)=2850.
(2)依题意,
S=(n+1)•1000-50•(1+2+3+…+n)
=(n+1)•1000-50•
| n(n+1) |
| 2 |
=-25n2+975n+1000,n∈N*.
(3)依题意,当月销售量S最大时,可获得最大利润.
由(2)知S=-25n2+975n+1000=-25(n2-39n)+1000.
从企业利益考虑,当n=19时,即该企业的广告费为19000元时,
月销售量S的最大值等于(19+1)×1000-50×=10500件,
此时月利润的最大值为105000元.
点评:本题重点考查了程序框图的识图、执行情况分析、函数的实际运用等知识,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
已知θ是三角形的一个内角,且sinθ+cosθ=
,则x2sinθ-y2cosθ=1表示( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则该函数图象( )
| π |
| 3 |
A、关于直线x=
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于点(
|
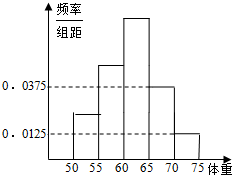 为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )
为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )| A、96 | B、32 | C、18 | D、48 |
某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( )
| A、60种 | B、70种 |
| C、80种 | D、120种 |
如图所示的程序输出的结果S为( )


| A、17 | B、19 | C、21 | D、23 |
设P点是曲线y=x3-
x+
上的任意一点,P点处切线倾斜角为α,则角α的取值范围是( )
| 3 |
| 2 |
| 3 |
A、[0,
| ||||
B、[0,
| ||||
C、[
| ||||
D、(
|