题目内容
设函数f(x)=cos(2x+
)+sin2x．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设A，B，C为△ABC的三个内角，若AB=1，sinB=
，求AC的长．
| π |
| 6 |
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设A，B，C为△ABC的三个内角，若AB=1，sinB=
| 1 |
| 3 |
考点：正弦定理的应用,两角和与差的正弦函数,正弦函数的单调性
专题：三角函数的求值
分析：利用两角差的余弦函数以及正弦函数化简函数为一个角的一个三角函数的形式，
（Ⅰ）利用正弦函数的单调增区间求解函数f（x）的单调递增区间；
（Ⅱ）利用第一问的结果求出C的正弦函数值，结合设A，B，C为△ABC的三个内角，若AB=1，sinB=
，利用正弦定理即可求AC的长．
（Ⅰ）利用正弦函数的单调增区间求解函数f（x）的单调递增区间；
（Ⅱ）利用第一问的结果求出C的正弦函数值，结合设A，B，C为△ABC的三个内角，若AB=1，sinB=
| 1 |
| 3 |
解答：
（本小题共13分）
解：f(x)=cos(2x+
)+sin2x
=cos2xcos
-sin2xsin
+sin2x=
cos2x+
sin2x=sin(2x+
)…（3分）
（I）令2kπ-
≤2x+
≤2kπ+
，k∈Z，则kπ-
≤x≤kπ+
，k∈Z
所以函数f（x）的单调递增区间为[kπ-
，kπ+
](k∈Z)．…（6分）
（II）由已知f(
)=sin(C+
)=
，…．（8分）
因为0＜C＜π，∴
＜C+
＜
所以C+
=
，C=
，所以sinC=
．…（10分）
在△ABC中，由正弦定理，
=
，得AC=
=
=
．…..（13分）
解：f(x)=cos(2x+
| π |
| 6 |
=cos2xcos
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
（I）令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
所以函数f（x）的单调递增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
（II）由已知f(
| C |
| 2 |
| π |
| 3 |
| ||
| 2 |
因为0＜C＜π，∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
所以C+
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| ||
| 2 |
在△ABC中，由正弦定理，
| AC |
| sinB |
| AB |
| sinC |
| AB•sinB |
| sinC |
| ||||
|
2
| ||
| 9 |
点评：本题考查两角和与差的三角函数，正弦定理的应用，考查三角形的解法，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
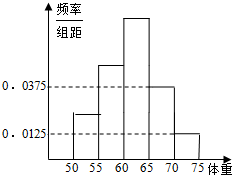为了了解高三学生的身体状况．抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则抽取的男生人数是（ ）| A、96 | B、32 | C、18 | D、48 |
设P点是曲线y=x3-
x+
上的任意一点，P点处切线倾斜角为α，则角α的取值范围是（ ）
| 3 |
| 2 |
| 3 |
A、[0，
| ||||
B、[0，
| ||||
C、[
| ||||
D、(
|
下列各个说法正确的是（ ）
| A、终边相同的角都相等 |
| B、钝角是第二象限的角 |
| C、第一象限的角是锐角 |
| D、第四象限的角是负角 |
下列选项中，p是q的必要不充分条件的是（ ）
| A、p：a+c＞b+d，q：a＞b且c＞d |
| B、p：a＞1，b＞1 q：f（x）=ax-b（1≠a＞0）的图象不过第二象限 |
| C、p：x=1，q：x2=x |
| D、p：a＞1，q：f（x）=logax（1≠a＞0）在（0，+∞）上为增函数 |