题目内容
设函数f（x）=
，则满足f（x）=
的x的值为 ．
|
| 1 |
| 4 |
考点：函数的值
专题：函数的性质及应用
分析：由已知中函数f（x）=
，分x＜1时和当x≥1时两种情况，讨论满足f（x）=
的x的值，最后综合讨论结果，可得答案．
|
| 1 |
| 4 |
解答：
解：当x＜1时，由f（x）=2-x=
，解得x=2（舍去），
当x≥1时，由f（x）=
-x=
，解得x=
，
综上所述，满足f（x）=
的x的值为
，
故答案为：
| 1 |
| 4 |
当x≥1时，由f（x）=
| 3 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
综上所述，满足f（x）=
| 1 |
| 4 |
| 5 |
| 4 |
故答案为：
| 5 |
| 4 |
点评：本题考查的知识点是函数的值，分段函数，分段函数分类讨论，是解答此类问题的一般方法．
练习册系列答案
相关题目
已知椭圆过点A（2，4），B（3，-1），则此椭圆的标准方程为（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
| D、以上都不对 |
已知扇形的面积为
π，半径是1，则扇形的圆心角是（ ）
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
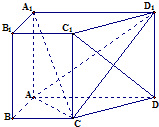如图，在直四棱柱ABCD-A1B1C1D1中，底面四边形ABCD是直角梯形，其中AB⊥AD，AB=BC=1且AD=