题目内容
1. 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上一点,且PA=AC,点E为PC的中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上一点,且PA=AC,点E为PC的中点.(1)求证:△PBC是直角三角形;
(2)求证:AE⊥平面PBC.
分析 (1)根据底面是圆,得到BC⊥AC,再根据PA⊥平面ABC得到PA⊥BC,即可证明BC⊥平面PAC,从而可证BC⊥PC,即可得证.
(2)由(1)可证BC⊥AE,由PA=AC,点E为PC的中点,可证PC⊥AE,即可得证AE⊥平面PBC.
解答 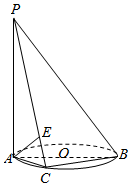 证明:(1)∵PA⊥⊙O所在的平面,BC?⊙O所在的平面,
证明:(1)∵PA⊥⊙O所在的平面,BC?⊙O所在的平面,
∴PA⊥BC,
又∵AB是⊙O的直径,C是⊙O上一点,
∴AC⊥BC,
∵PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥PC,
∴△PBC是直角三角形.
(2)∵由(1)可得BC⊥平面PAC.
又∵AE在平面PAC内,
∴BC⊥AE.
∵PA=AC,点E为PC的中点
∴PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
点评 本题综合考查了线面垂直的判定与性质定理等基础知识与基本技能方法,考查了空间想象能力、推理能力和计算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.已知A(a,2),B(1,b)为平面直角坐标系中第一象限的两点,C(4,-1),O为坐标原点,若$\overrightarrow{OA}$与$\overrightarrow{OB}$在$\overrightarrow{OC}$方向上的投影相同,则2$\sqrt{a}$+$\sqrt{b}$的最大值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
10.设集合A={(x,y)|x2+y2=16,x∈Z,y∈Z},则集合A的子集个数为( )
| A. | 8 | B. | 32 | C. | 16 | D. | 15 |
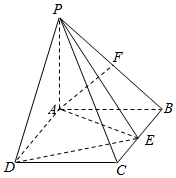 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.