题目内容
12.若一个椭圆的内接正方形有两边分别经过它的两个焦点,则此椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
分析 由题意可知:椭圆的通径长$\frac{2{b}^{2}}{a}$,则$\frac{2{b}^{2}}{a}$=2c,由椭圆的离心率e=$\frac{c}{a}$,求得e2+e-1=0,根据椭圆的离心率取值范围,即可求得椭圆的离心率.
解答 解:假设椭圆的焦点在x轴上,设椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由椭圆与正方形的对称性可知:正方形的一边长为椭圆焦距为2c,
另一边长为通径长$\frac{2{b}^{2}}{a}$,
则$\frac{2{b}^{2}}{a}$=2c,
∴a2-c2=ac,由椭圆的离心率e=$\frac{c}{a}$,
整理得:e2+e-1=0,
解得:e=$\frac{-1±\sqrt{5}}{2}$,
由椭圆的离心率e>0,
则e=$\frac{\sqrt{5}-1}{2}$,
故选C.
点评 本题考查椭圆的离心率的应用,考查椭圆的通径长度,考查计算能力,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
17.已知A,B,C三点在球O的球面上,AB=BC=CA=3,且球心O到平面ABC的距离等于球半径的$\frac{1}{3}$,则球O的表面积为( )
| A. | 36π | B. | 4π | C. | $\frac{27}{4}$π | D. | $\frac{27}{2}$π |
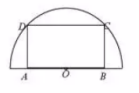 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、