题目内容
已知直线y=k（x-2）+6与双曲线x2-y2=1恒有公共点则k的取值范围是 ．
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：联立直线方程与双曲线方程，利用判别式得到不等式组，求解即可．
解答：
解：把y=k（x-2）+6代入x2-y2=1得 x2-[k（x-2）+6]2=1
整理得 （1-k2）x2-2k（6-2k）x+（24k-4k2-37）=0 直线与双曲线恒有公共点，
则△=[2k（6-2k）]2-4（1-k2）（24k-4k2-37）≥0
3k2-24k+37≥0，
解得k≥4+
或 k≤4-
．
故答案为：k≥4+
或 k≤4-
．
解：把y=k（x-2）+6代入x2-y2=1得 x2-[k（x-2）+6]2=1 整理得 （1-k2）x2-2k（6-2k）x+（24k-4k2-37）=0 直线与双曲线恒有公共点，
则△=[2k（6-2k）]2-4（1-k2）（24k-4k2-37）≥0
3k2-24k+37≥0，
解得k≥4+
| ||
| 3 |
| ||
| 3 |
故答案为：k≥4+
| ||
| 3 |
| ||
| 3 |
点评：本题考查直线与双曲线的位置关系，交点个数问题，考查计算能力．
练习册系列答案
相关题目
已知函数f（x）=2
sin（π-x）•cosx-1+2cos2x，其中x∈R，则下列结论中正确的是（ ）
| 3 |
A、f（x）的一条对称轴是x=
| ||||
B、f（x）在[-
| ||||
| C、f（x）是最小正周期为π的奇函数 | ||||
D、将函数y=2sin2x的图象左移
|
如图所示，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠BAD=∠ABC=90°，PA=AD=2，AB=BC=1．试问在线段PA上是否存在一点M到平面PCD的距离为
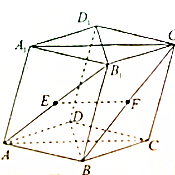如图所示，四棱柱ABCD-A1B1C1D1中，E、F分别是AB1、BC1的中点，下列结论中，正确的是（ ）| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |