题目内容
已知函数f(x)=
,则函数g(x)=xf(x)-9的零点个数是( )
|
| A、6 | B、7 | C、8 | D、9 |
考点:函数零点的判定定理
专题:函数的性质及应用,导数的概念及应用
分析:函数g(x)=xf(x)-9的零点个数
即y=f(x)-
的零点个数
可转化为:f(x)与h(x)=
的交点个数,
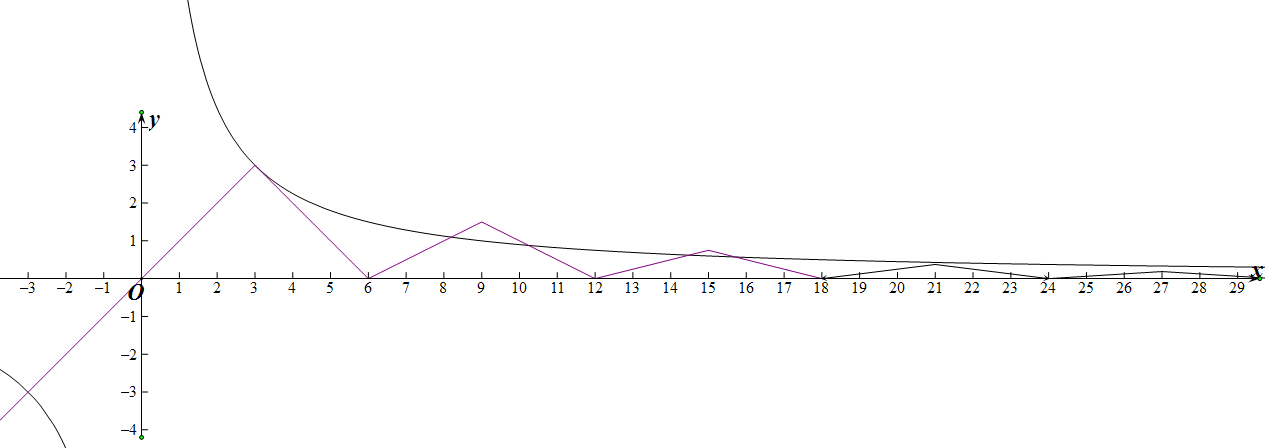
画出图象,结合图象,利用导数判断即可.
即y=f(x)-
| 9 |
| x |
可转化为:f(x)与h(x)=
| 9 |
| x |
画出图象,结合图象,利用导数判断即可.
解答:
解:∵函数f(x)=
,
∴函数g(x)=xf(x)-9的零点个数
即y=f(x)-
的零点个数
可转化为:f(x)与h(x)=
的交点个数,
∵h′(x)=-
,h′(3)=-1,点(3,3)的切线为:y=6-x,
∴再点(3,3)附近没有其他的交点,
∴从图中可以判断出:f(x)与h(x)=
的交点个数为6,
故选:A
|
∴函数g(x)=xf(x)-9的零点个数
即y=f(x)-
| 9 |
| x |
可转化为:f(x)与h(x)=
| 9 |
| x |
∵h′(x)=-
| 9 |
| x2 |
∴再点(3,3)附近没有其他的交点,
∴从图中可以判断出:f(x)与h(x)=
| 9 |
| x |
故选:A

点评:本题考查了分段函数,复杂函数的零点问题,利用函数图象判断即可,属于难题,关键是画图,必要时可以运用导数判断.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
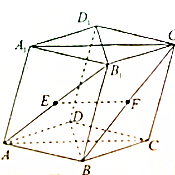 如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )
如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
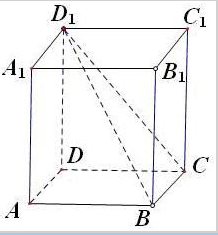 设正方体ABCD-A1B1C1D1的棱长为1,则:
设正方体ABCD-A1B1C1D1的棱长为1,则: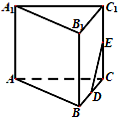 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=