题目内容
12.已知圆心为C的圆经过点A(1,1)和点B(2,-2)且圆心C在直线l:x+3y+3=0上.(1)求圆C的方程.
(2)若P是直线3x+4y-21=0上的动点,PM,PN是圆C的两条切线,M,N为切点,设|PC|=t,把四边形PMCN的面积S表示为t的函数,并求出该函数的最小值.
分析 (1)利用待定系数法,求出圆心坐标,即可求圆C的方程.
(2)利用勾股定理求出PM,即可求出S,t的最小值为C到直线的距离,即可求出该函数的最小值.
解答 解:(1)设圆心为(-3a-3,a),则(-3a-3-1)2+(a-1)2=(-3a-3-2)2+(a+2)2,∴a=-1,
∴圆C的方程为x2+(y+1)2=5;
(2)PM=$\sqrt{{t}^{2}-5}$,∴S=2×$\frac{1}{2}×PM×\sqrt{5}$=$\sqrt{5}•\sqrt{{t}^{2}-5}$,
t的最小值为C到直线的距离,即d=$\frac{|0-4-21|}{5}$=5,
∴S的最小值=$\sqrt{5}•\sqrt{25-5}$=10.
点评 本题考查圆的方程,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
2.函数f(x)是定义在R上的偶函数,且在[0,+∞)上是增函数,若f(a)≤f(2),则实数a的取值范围是( )
| A. | (-∞,2] | B. | (0,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
3.如果集合A={x|x>-1},那么( )
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
20.过点$P(2\sqrt{3},3)$且倾斜角为30o的直线方程为( )
| A. | .$y+4\sqrt{3}=3x$ | B. | .$y=x-\sqrt{3}$ | C. | $3y-3=\sqrt{3}x$ | D. | .$y-\sqrt{3}=\sqrt{3}x$ |
4.已知z=(m-3)+(m+1)i在复平面内对应的点在第二象限,则实数m的取值范围是( )
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
2.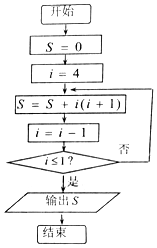 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )
 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | 40 | B. | 38 | C. | 32 | D. | 20 |
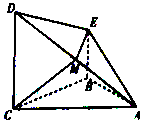 如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.