题目内容
1.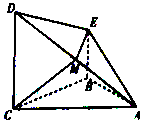 如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
如图,在四棱锥A-BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.(Ⅰ)证明:EM∥平面ABC;
(Ⅱ)若CD=2,求四棱锥A-BCDE的体积.
分析 (Ⅰ)取线段AC的中点F,连接BF.通过BF⊥AC,CD⊥BF,证明BF⊥平面ACD,推出EM∥BF,然后证明EM∥平面ABC.
(Ⅱ)连接MF,证明BE∥平面ACD,推出BE∥MF,证明四边形BEMF为平行四边形,然后证明CD⊥AB,推出AB⊥平面BCDE,求解棱锥的底面面积,求解几何体的体积.
解答 (Ⅰ)证明:取线段AC的中点F,连接BF.
因为AB=BC,所以BF⊥AC,
因为CD⊥平面ABC,所以CD⊥BF,又AC∩CD=C,所以BF⊥平面ACD,
因为EM⊥平面ACD,所以EM∥BF,又EM?平面ABC,BF?平面ABC,
所以EM∥平面ABC.
(Ⅱ)解:连接MF,因为BE∥CD,BE?平面ACD,CD?平面ACD,所以BE∥平面ACD,
又平面BEMF∩平面ACD=MF,所以BE∥MF,
由(Ⅰ)知EM∥BF,所以四边形BEMF为平行四边形,所以BE=MF.
因为F是AC的中点,所以M是AD的中点,
所以$BE=MF=\frac{1}{2}CD=1$.
因为CD⊥平面ABC,所以CD⊥AB,
又BC⊥AB,所以AB⊥平面BCDE,
所以四棱锥A-BCDE的体积${V_{A-BCDE}}=\frac{1}{3}{S_{BCDE}}•AB=\frac{1}{3}×\frac{1}{2}×(1+2)×2×2=2$.
点评 本题考查直线与平面平行的判定定理以及性质定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
11.某人通过普通话二级测试的概率是$\frac{1}{3}$,他连线测试3次,那么其中恰有1次通过的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
9.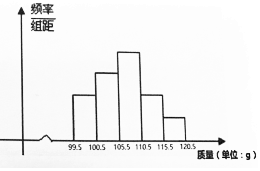 检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
 检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )
检测600个某产品的质量(单位:g),得到的直方图中,前三组的长方形的高度成等差数列,后三组对应的长方形的高度成公比为0.5的等比数列,已知检测的质量在100.5-105.5之间的产品数为150,则质量在115.5-120.5的长方形高度为( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{30}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{60}$ |
13.锥体中,平行于底面的两个平面把锥体的体积三等分,这时高被分成三段的长自上而下的比为( )
| A. | 1:$\root{3}{2}$:$\root{3}{3}$ | B. | 1:2:3 | C. | 1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$) | D. | 1:($\root{3}{2}$-1):($\root{3}{3}$-$\root{3}{2}$) |
4.从1,3,5,7,9中任取3个数字,从2,4,6,8中任取2个数字,组成没有重复数字的五位数,则组成的五位数是偶数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.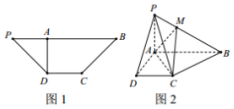 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.