题目内容
2.函数f(x)是定义在R上的偶函数,且在[0,+∞)上是增函数,若f(a)≤f(2),则实数a的取值范围是( )| A. | (-∞,2] | B. | (0,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
分析 利用函数f(x)是偶函数,将不等式f(a)≤f(2),等价转化为f(|a|)≤f(2),然后利用函数在[0,+∞)上是单调增函数,进行求解.
解答 解:∵函数f(x)是偶函数,∴不等式f(a)≤f(2),等价转化为f(|a|)≤f(2),
∵函数在[0,+∞)上是单调增函数,
∴|a|≤2,
解得-2≤a≤2,
故选C.
点评 本题考查函数的奇偶性与单调性综合应用,解决本题的关键是利用函数的性质将不等式进行转化.若函数为偶函数,则f(a)<f(b)等价为f(|a|)<f(|b|).

练习册系列答案
相关题目
14.执行如图所示的程序框图,那么输出的S为( )


| A. | -2 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | 3 |
11.某人通过普通话二级测试的概率是$\frac{1}{3}$,他连线测试3次,那么其中恰有1次通过的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.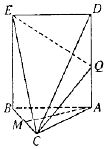 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点