题目内容
4．已知z=（m-3）+（m+1）i在复平面内对应的点在第二象限，则实数m的取值范围是（ ）| A． | （-3，1） | B． | （-1，3） | C． | （1，+∞） | D． | （-∞，-3） |
分析 利用复数的几何意义、不等式的解法即可得出．
解答 解：z=（m-3）+（m+1）i在复平面内对应的点在第二象限，
∴m-3＜0，m+1＞0，解得-1＜m＜3．
则实数m的取值范围是（-1，3）．
故选：B．
点评 本题考查了复数的几何意义、不等式的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
14．执行如图所示的程序框图，那么输出的S为（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | $\frac{4}{3}$ | D． | 3 |
已知f（x）为定义在R上的奇函数，当x＞0时，f（x）为二次函数，且满足f（2）=1，f（x）在x轴上的两个交点为（1，0）、（3，0）．
9．
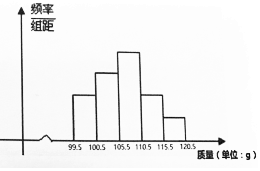检测600个某产品的质量（单位：g），得到的直方图中，前三组的长方形的高度成等差数列，后三组对应的长方形的高度成公比为0.5的等比数列，已知检测的质量在100.5-105.5之间的产品数为150，则质量在115.5-120.5的长方形高度为（ ）
检测600个某产品的质量（单位：g），得到的直方图中，前三组的长方形的高度成等差数列，后三组对应的长方形的高度成公比为0.5的等比数列，已知检测的质量在100.5-105.5之间的产品数为150，则质量在115.5-120.5的长方形高度为（ ）| A． | $\frac{1}{12}$ | B． | $\frac{1}{30}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{60}$ |
如图，四边形ABCD是边长为$\sqrt{2}$的正方形，CG⊥平面ABCD，DE∥BF∥CG，$DE=BF=\frac{3}{5}CG$．P为线段EF的中点，AP与平面ABCD所成角为60°．在线段CG上取一点H，使得$GH=\frac{3}{5}CG$．
13．锥体中，平行于底面的两个平面把锥体的体积三等分，这时高被分成三段的长自上而下的比为（ ）
| A． | 1：$\root{3}{2}$：$\root{3}{3}$ | B． | 1：2：3 | C． | 1：（$\sqrt{2}$-1）：（$\sqrt{3}$-$\sqrt{2}$） | D． | 1：（$\root{3}{2}$-1）：（$\root{3}{3}$-$\root{3}{2}$） |
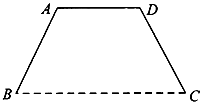某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门BADC （如图），设计要求彩门的面积为S （单位：m2）•高为h（单位：m）（S，h为常数），彩门的下底BC固定在广场地面上，上底和两腰由不锈钢支架构成，设腰和下底的夹角为α，不锈钢支架的长度和记为l．