题目内容
20．过点$P（2\sqrt{3}，3）$且倾斜角为30o的直线方程为（ ）| A． | .$y+4\sqrt{3}=3x$ | B． | .$y=x-\sqrt{3}$ | C． | $3y-3=\sqrt{3}x$ | D． | .$y-\sqrt{3}=\sqrt{3}x$ |
分析 由直线的倾斜角求出直线的斜率，代入直线方程的点斜式得答案．
解答 解：∵直线的倾斜角为30°，∴其斜率为tan30°=$\frac{\sqrt{3}}{3}$，
由直线过点（2$\sqrt{3}$，3），
∴直线方程为y-3=$\frac{\sqrt{3}}{3}$（x-2$\sqrt{3}$），
即y=$\frac{\sqrt{3}}{3}$x+1，$\sqrt{3}$x-3y+3=0，
故选：C．
点评 本题考查待定系数法求直线方程，考查了直线方程的点斜式，是基础题．
练习册系列答案
相关题目
如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，∥DC，AD⊥DC，PD⊥平面ABCD，AB=PD=DA=2PE，CD=3PE，F是CE的中点．
11．某人通过普通话二级测试的概率是$\frac{1}{3}$，他连线测试3次，那么其中恰有1次通过的概率是（ ）
| A． | $\frac{4}{9}$ | B． | $\frac{1}{9}$ | C． | $\frac{4}{27}$ | D． | $\frac{2}{9}$ |
已知f（x）为定义在R上的奇函数，当x＞0时，f（x）为二次函数，且满足f（2）=1，f（x）在x轴上的两个交点为（1，0）、（3，0）．
9．
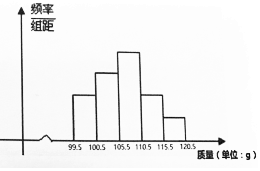检测600个某产品的质量（单位：g），得到的直方图中，前三组的长方形的高度成等差数列，后三组对应的长方形的高度成公比为0.5的等比数列，已知检测的质量在100.5-105.5之间的产品数为150，则质量在115.5-120.5的长方形高度为（ ）
检测600个某产品的质量（单位：g），得到的直方图中，前三组的长方形的高度成等差数列，后三组对应的长方形的高度成公比为0.5的等比数列，已知检测的质量在100.5-105.5之间的产品数为150，则质量在115.5-120.5的长方形高度为（ ）| A． | $\frac{1}{12}$ | B． | $\frac{1}{30}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{60}$ |
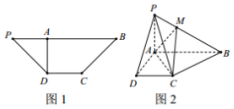如图1，在等腰梯形PDCB中，PB∥DC，PB=3，DC=1，∠DPB=45°，DA⊥PB于点A，将△PAD沿AD折起，构成如图2所示的四棱锥P-ABCD，点M的棱PB上，且PM=$\frac{1}{2}$MB．