题目内容
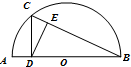如图，在半圆O中，C是圆O上一点，直径AB⊥CD，垂足为D，DE⊥BC，垂足为E，若AB=6，AD=1，则CE•BC=考点：与圆有关的比例线段
专题：直线与圆,推理和证明
分析：由已知条件利用垂直径定理和相交弦定理得CD2=AD•BD，从而得CD=
，CB=
=
，由DE⊥BC，利用等积法能求出DE=
，由勾股定理得CE=
，由此能求出CE•BC．
| 5 |
| CD2+BD2 |
| 30 |
5
| ||
| 6 |
| ||
| 6 |
解答：
解：∵C是圆O上一点，直径AB⊥CD，垂足为D，AB=6，AD=1，
∴CD2=AD•BD=1×（6-1）=5，解得CD=
，
∴CB=
=
=
，
∵DE⊥BC，垂足为E，
∴
CD•BD=
BC•DE，解得DE=
=
=
，
∴CE=
=
=
，
∴CE•BC=
×
=5．
故答案为：5．
∴CD2=AD•BD=1×（6-1）=5，解得CD=
| 5 |
∴CB=
| CD2+BD2 |
| 5+25 |
| 30 |
∵DE⊥BC，垂足为E，
∴
| 1 |
| 2 |
| 1 |
| 2 |
| BD•CD |
| BC |
5×
| ||
|
5
| ||
| 6 |
∴CE=
| CD2-DE2 |
5-
|
| ||
| 6 |
∴CE•BC=
| ||
| 6 |
| 30 |
故答案为：5．
点评：本题考查两线段乘积的求法，是中档题，解题时要认真审题，注意垂径定理和相交弦定理的合理运用．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
已知f（x）=
，则
的值是（ ）
| x |
| lim |
| △x→0 |
| f(x-△x)-f(x) |
| △x |
A、-
| ||||
B、
| ||||
C、-
|
若空间几何体的三视图如图所示，则该几何体体积为（ ）
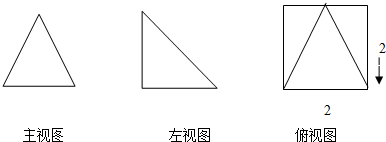
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
已知一个几何体的三视图如图所示，那么该几何体的表面积是（ ）
A、5+
| ||
| B、7 | ||
C、7+
| ||
| D、9 |