题目内容
在长方形ABCD中,AB=4,AD=2,O时它的中心,过点O任作一直线与长方形的边交于M,N两点,P是长方形边界上任意一点,则
•
的最大值为 .
| PM |
| PN |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,建立直角坐标系.
+
=
.于是
•
=(
-
)•(
-
)=
•
+
2,当且仅当点P为矩形的一个顶点,点M,N分别为边AB、CD的中点时取得最大值.
| OM |
| ON |
| 0 |
| PM |
| PN |
| OM |
| OP |
| ON |
| OP |
| OM |
| ON |
| OP |
解答:
解:如图所示,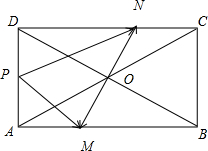 建立直角坐标系.
建立直角坐标系.
+
=
.
则
•
=(
-
)•(
-
)
=
•
-
•(
+
)+
2
=
•
+
2
≤(
)2-12=4,
当且仅当点P为矩形的一个顶点,点M,N分别为边AB、CD的中点时取等号.
故最大值为:4.
故答案为:4.
 建立直角坐标系.
建立直角坐标系.| OM |
| ON |
| 0 |
则
| PM |
| PN |
| OM |
| OP |
| ON |
| OP |
=
| OM |
| ON |
| OP |
| OM |
| ON |
| OP |
=
| OM |
| ON |
| OP |
≤(
| 5 |
当且仅当点P为矩形的一个顶点,点M,N分别为边AB、CD的中点时取等号.
故最大值为:4.
故答案为:4.
点评:本题考查了向量的数量积运算性质、向量的三角形法则、向量共线定理,考查了推理能力与计算能力,考查了数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
等比数列{an}的前n项和为Sn,已知a1=2014,且an+2an+1+an+2=0(n∈N*),则S2014=( )
| A、2013 | B、2014 |
| C、1 | D、0 |
设f(x)=lg(
+a)是奇函数,则a的取值( )
| 2 |
| 1+x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
已知数列{an}满足a1=0,an+1=an+2n,那么a2009的值是( )
| A、20092 |
| B、2008×2007 |
| C、2009×2010 |
| D、2008×2009 |
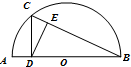 如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=
如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=