题目内容
已知函数f(x)=
,若任意?x∈N*,f(x)≥f(5)恒成立,则a的取值范围是 .
| 2x+1 |
| x-a |
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:将函数变形,由任意?x∈N*,f(x)≥f(5)恒成立,可得
或
或2a+1=0,由此可求a的取值范围.
|
|
解答:
解:f(x)=
=2+
.
∵任意?x∈N*,f(x)≥f(5)恒成立,
∴
或
或2a+1=0,
∴a=-
或5<a<6.
故答案为:a=-
或5<a<6.
| 2x+1 |
| x-a |
| 2a+1 |
| x-a |
∵任意?x∈N*,f(x)≥f(5)恒成立,
∴
|
|
∴a=-
| 1 |
| 2 |
故答案为:a=-
| 1 |
| 2 |
点评:本题主要考查不等式恒成立问题,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
如图是一个体积为10的空间几何体的三视图,则图中x的值为( )


| A、2 | B、3 | C、4 | D、5 |
设Sn为等差数列{an}的前n项和.若a4<0,a5>|a4|,则使Sn>0成立的最小正整数n为( )
| A、6 | B、7 | C、8 | D、9 |
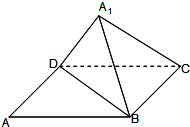 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.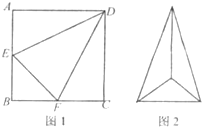 如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为
如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为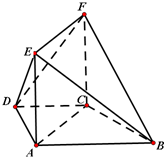 如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.