题目内容
已知正数x，y，z满足x2+y2+z2=6．
（Ⅰ）求x+2y+z的最大值；
（Ⅱ）若不等式|a+1|-2a≥x+2y+z对满足条件的x，y，z恒成立，求实数a的取值范围．
（Ⅰ）求x+2y+z的最大值；
（Ⅱ）若不等式|a+1|-2a≥x+2y+z对满足条件的x，y，z恒成立，求实数a的取值范围．
考点：柯西不等式在函数极值中的应用,函数恒成立问题,绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：（Ⅰ）运用柯西不等式，（x2+y2+z2）（12+22+12）≥（x+2y+z）2，即可得到最大值；
（Ⅱ）不等式|a+1|-2a≥x+2y+z对满足条件的x，y，z恒成立即为|a+1|-2a≥（x+2y+z）max=6，对a+1讨论，即可解得a的取值范围．
（Ⅱ）不等式|a+1|-2a≥x+2y+z对满足条件的x，y，z恒成立即为|a+1|-2a≥（x+2y+z）max=6，对a+1讨论，即可解得a的取值范围．
解答：
解：（Ⅰ）由于x2+y2+z2=6，
由柯西不等式，（x2+y2+z2）（12+22+12）≥（x+2y+z）2，
即有（x+2y+z）2≤36，
又x、y、z是正数，
则x+2y+z≤6即x+2y+z的最大值为6，
当且仅当
=
=
，即当x=z=1，y=2时取得最大值；
（Ⅱ）由题意及（Ⅰ）得，|a+1|-2a≥（x+2y+z）max=6，
即：a+1≥0且a+1-2a≥6①a+1＜0，且-a-1-2a≥6，②
即a≥-1，且a≤-5；a＜-1且a≤-
．
解得：a无解或a≤-
．
综上，实数a的取值范围为（-∞，-
]．
由柯西不等式，（x2+y2+z2）（12+22+12）≥（x+2y+z）2，
即有（x+2y+z）2≤36，
又x、y、z是正数，
则x+2y+z≤6即x+2y+z的最大值为6，
当且仅当
| x |
| 1 |
| y |
| 2 |
| z |
| 1 |
（Ⅱ）由题意及（Ⅰ）得，|a+1|-2a≥（x+2y+z）max=6，
即：a+1≥0且a+1-2a≥6①a+1＜0，且-a-1-2a≥6，②
即a≥-1，且a≤-5；a＜-1且a≤-
| 7 |
| 3 |
解得：a无解或a≤-
| 7 |
| 3 |
综上，实数a的取值范围为（-∞，-
| 7 |
| 3 |
点评：本小题主要考查柯西不等式、绝对值的意义、绝对值不等式、恒成立问题等基础知识，考查运算求解能力，分类讨论思想．
练习册系列答案
相关题目
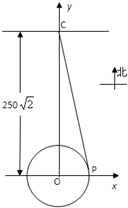某城市交通规划中，拟在以点O为圆心，半径为50m的高架圆形车道外侧P处开一个出口，以与圆形道相切的方式，引申一条直道连接到距圆形道圆心O正北250
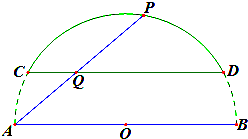某房地产开发商在其开发的一个小区前面建了一个弓形景观湖，如图，该弓形所在的圆是以AB为直径的圆，已知AB=300m，CD与AB平行且它们之间的距离为50