题目内容
从x轴上一点A分别向函数f(x)=-x3与函数g(x)=
引不是水平方向的切线l1和l2,两切线l1、l2分别与y轴相交于点B和点C,O为坐标原点,记△OAB的面积为S1,△OAC的面积为S2,则S1+S2的最小值为 .
| 2 |
| |x3|+x3 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:分别求出两个函数的导函数,设出两切点坐标,得到两切线方程,设出A的坐标并代入切线方程,把两切线与y轴的交点用A的坐标表示,求出面积,然后利用导数求最小值.
解答:
解:由f(x)=-x3,g(x)=
=x-3(x>0),
得f′(x)=-3x2,g′(x)=-3x-4,
设点为A(x0,0),
则l1和l2的方程分别为y+x13=-3x12(x-x1),y-x2-3=-3x-4(x-x2),
分别代入A(x0,0)并整理得,
4x1-3x0=0,2x2-3x0=0,解得:x1=
x0,x2=
x0.
∴l1,l2与y轴的交点坐标分别为(0,
x03),(0,
x03).
∴S=
(
x0-2+
x04)=
x0-2+
x04.
S′=-
x0-3+
x03.
由S′=0,解得x02=
.
∴当x0∈(-∞,-
),(
,+∞)时,S′>0;
当x0∈(-
,
)时,S′<0.
∴当x0=
时S有最小值为8.
故答案为:8.
| 2 |
| |x3|+x3 |
得f′(x)=-3x2,g′(x)=-3x-4,
设点为A(x0,0),
则l1和l2的方程分别为y+x13=-3x12(x-x1),y-x2-3=-3x-4(x-x2),
分别代入A(x0,0)并整理得,
4x1-3x0=0,2x2-3x0=0,解得:x1=
| 3 |
| 4 |
| 3 |
| 2 |
∴l1,l2与y轴的交点坐标分别为(0,
| 256 |
| 27 |
| 27 |
| 4 |
∴S=
| 1 |
| 2 |
| 256 |
| 27 |
| 27 |
| 4 |
| 128 |
| 27 |
| 27 |
| 8 |
S′=-
| 256 |
| 27 |
| 27 |
| 2 |
由S′=0,解得x02=
| 8 |
| 9 |
∴当x0∈(-∞,-
2
| ||
| 3 |
2
| ||
| 3 |
当x0∈(-
2
| ||
| 3 |
2
| ||
| 3 |
∴当x0=
2
| ||
| 3 |
故答案为:8.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,考查了学生的计算能力,是压轴题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
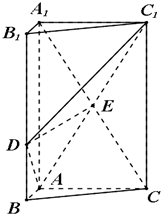 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=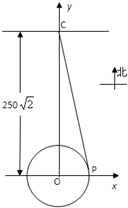 某城市交通规划中,拟在以点O为圆心,半径为50m的高架圆形车道外侧P处开一个出口,以与圆形道相切的方式,引申一条直道连接到距圆形道圆心O正北250
某城市交通规划中,拟在以点O为圆心,半径为50m的高架圆形车道外侧P处开一个出口,以与圆形道相切的方式,引申一条直道连接到距圆形道圆心O正北250