题目内容
给出以下命题:
①?x∈R,sinx+cosx>1;
②?x∈R,x2-x+1<0;
③“x>1”是“|x|>1”的充分不必要条件;
④若
•
=0,则|
|=|
|=0.
其中假命题的个数是( )
①?x∈R,sinx+cosx>1;
②?x∈R,x2-x+1<0;
③“x>1”是“|x|>1”的充分不必要条件;
④若
| a |
| b |
| a |
| b |
其中假命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:举出反例x=0,可判断①的真假;根据函数y=x2-x+1的图象是开口朝上,且与x轴无交点的抛物线,可判断②;利用充要条件的定义可判断③;根据向量垂直的充要条件,可判断④.
解答:
解:当x=0时,sinx+cosx=1,故①为假命题;
函数y=x2-x+1的图象是开口朝上,且与x轴无交点的抛物线,故x2-x+1>0恒成立,故②为假命题;
“x>1”⇒“|x|>1”成立,“x>1”?“|x|>1”不成立,故“x>1”是“|x|>1”成立的充分不必要条件,故③为真命题;
若
•
=0,则若
⊥
,|
|=|
|=0不一定成立,故④为假命题;
综上所述,假命题的个数是3个,
故选:D
函数y=x2-x+1的图象是开口朝上,且与x轴无交点的抛物线,故x2-x+1>0恒成立,故②为假命题;
“x>1”⇒“|x|>1”成立,“x>1”?“|x|>1”不成立,故“x>1”是“|x|>1”成立的充分不必要条件,故③为真命题;
若
| a |
| b |
| a |
| b |
| a |
| b |
综上所述,假命题的个数是3个,
故选:D
点评:本题以命题的真假判断为载体考查了三角函数的图象和性质,二次函数的图象和性质,充要条件的定义及向量垂直的充要条件,属于基础题.

练习册系列答案
相关题目
已知点A(-3,1,-4),B(3,-5,10)则线段AB的中点M的坐标为( )
| A、(0,-4,6) |
| B、(0,-2,3) |
| C、(0,2,3) |
| D、(0,-2,6) |
已知圆的方程是(x-2)2+(y-3)2=4,则点P(-3,-2)满足( )
| A、是圆心 | B、在圆上 |
| C、在圆内 | D、在圆外 |
已知a,b,c∈R,a+b+c=0,abc>0,T=
+
+
,则( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、T>0 | B、T<0 |
| C、T=0 | D、T≥0 |
已知sin(
+α)=
,则cos(
+α)的值为( )
| π |
| 3 |
| 4 |
| 5 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若三点A(2,3),B(3,4),C(a,b)共线,则有( )
| A、a=3,b=-5 |
| B、a-b+1=0 |
| C、2a-b=3 |
| D、a-2b=0 |
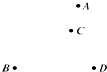 如图A、B、C、D是某油田的四口油井,计划建三条路,将这四口油井连结起来(每条路只连结两口油井),那么不同的建路方案有( )
如图A、B、C、D是某油田的四口油井,计划建三条路,将这四口油井连结起来(每条路只连结两口油井),那么不同的建路方案有( )| A、12种 | B、14种 |
| C、16种 | D、18种 |
数列{an}中,a1=3,a2=6,an+2=an+1-an,那么a6=( )
| A、-2 | B、-3 | C、-6 | D、-8 |