题目内容
如图，已知向量| AC |
| AB |
| AD |
| AC |
| a |
| DB |
| b |
| a |
| b |
| a |
| b |
（1）求线段AB的长；
（2）过点C作CH⊥AB，垂足为H，若
| AH |
| a |
| b |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）根据向量的加法运算，可得到
=
(
+
)，根据向量
，
的长度及夹角可求出
2，从而求出|
|；
（2）根据图形知
与
共线，所以存在实数k，使得
=k
，从而可得到λ=μ，
=
+
=-
+λ
+μ
=（λ-1）
+λ
，因为CH⊥AB，所以
•
=0，所以[（λ-1）
+λ
]•[
(
+
)]=
[(λ-1)
2+(2λ-1)
•
+λ
2]=0，解出λ即可．
| AB |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| AB |
| AB |
（2）根据图形知
| AH |
| AB |
| AH |
| AB |
| CH |
| CA |
| AH |
| a |
| a |
| b |
| a |
| b |
| CH |
| AB |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| a |
| a |
| b |
| b |
解答：
解：（1）由已知条件得：
=
(
+
)；
∴
2=
(
2+2
•
+
2)=
；
∴|
|=
，即线段AB的长为
；
（2）向量
与
共线，∴存在实数k，使
=k
=k[
(
+
)]=
+
=λ
+μ
；
∴λ=μ；
∵CH⊥AB，即
⊥
；
∴
•
=(
+
)•
=[(λ-1)
+λ
]•[
(
+
)]=0；
∴解得λ=μ=
．
| AB |
| 1 |
| 2 |
| a |
| b |
∴
| AB |
| 1 |
| 4 |
| a |
| a |
| b |
| b |
| 7 |
| 4 |
∴|
| AB |
| ||
| 2 |
| ||
| 2 |
（2）向量
| AH |
| AB |
| AH |
| AB |
| 1 |
| 2 |
| a |
| b |
| k |
| 2 |
| a |
| k |
| 2 |
| b |
| a |
| b |
∴λ=μ；
∵CH⊥AB，即
| CH |
| AB |
∴
| CH |
| AB |
| CA |
| AH |
| AB |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
∴解得λ=μ=
| 5 |
| 7 |
点评：考查向量数量积的运算，共线向量基本定理，平面向量基本定理，两非零向量垂直的充要条件．
练习册系列答案
相关题目
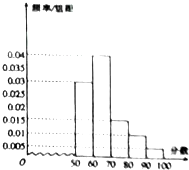在一次物理竞赛中，学生成绩均在内[50，100），相应的频率分布直方图如图，已知成绩在[60，70）的学生有40人，则成绩在[70，90）的人数为（ ）