题目内容
若二项展开式(2x-
)n的各项系数的绝对值之和为729,则展开式中的常数项是( )
| 1 | ||
|
| A、60 | B、45 | C、35 | D、30 |
考点:二项式系数的性质
专题:二项式定理
分析:根据二项展开式(2x-
)n的各项系数的绝对值和求出n的值,再求展开式中常数项是多少.
| 1 | ||
|
解答:
解:∵二项展开式(2x-
)n的各项系数的绝对值之和为729,
∴3n=729,解得n=6;
∴(2x-
)6展开式中
Tr+1=
•(2x)6-r•(-
)r=(-1)r•26-r•
•x6-
r,
令6-
r=0,解得r=4;
∴常数项是T4+1=(-1)4•26-4•
=60.
故选:A.
| 1 | ||
|
∴3n=729,解得n=6;
∴(2x-
| 1 | ||
|
Tr+1=
| C | r 6 |
| 1 | ||
|
| C | r 6 |
| 3 |
| 2 |
令6-
| 3 |
| 2 |
∴常数项是T4+1=(-1)4•26-4•
| C | 4 6 |
故选:A.
点评:本题考查了二项式定理的应用问题,解题时应熟记二项式展开式与通项公式是什么,属于基础题目.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
设Sn是等比数列{an}的前n项和,且32a2+a7=0,则
=( )
| S5 |
| S2 |
| A、11 | B、5 | C、-8 | D、-11 |
将一根长为3米的绳子拉直后在任意位置剪断,分为两段,那么这两段绳子的长都不小于1米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
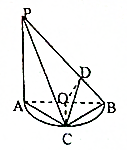 如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=