题目内容
如果-1，a，b，c，-4成等比数列，那么（ ）
| A、b=2，ac=4 |
| B、b=2，ac=-4 |
| C、b=-2，ac=4 |
| D、b=-2，ac=-4 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由等比数列的性质可得b2=ac=（-1）（-4），可得ac和b的值，验证可得．
解答：
解：由题意可得b2=ac=（-1）（-4），
∴ac=4，b=±2，
当b=2时，又可得a2=-1×b=-2矛盾，
∴b=-2，
故选：C
∴ac=4，b=±2，
当b=2时，又可得a2=-1×b=-2矛盾，
∴b=-2，
故选：C
点评：本题考查等比数列的通项公式，属基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
点A是抛物线C1：y2=2px（p＞0）与双曲线C2：
-
=1（a＞0，b＞0）的一条渐近线的交点（异于原点），若点A到抛物线C1的准线的距离为p，则双曲线C2的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行以下程序框图，所得的结果为（ ）
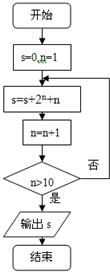
| A、1067 | B、2100 |
| C、2101 | D、4160 |
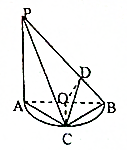如图，PA垂直⊙O所在平面ABC，AB为⊙O的直径，PA=AB，BD=