题目内容
求函数的定义域：
（1）已知函数y=F（x）定义域为[1，3]，求函数y=F（2x+1）的定义域；
（2）已知函数y=F（2x+1）的定义域为[1，3]，求函数y=F（x）的定义域．
（1）已知函数y=F（x）定义域为[1，3]，求函数y=F（2x+1）的定义域；
（2）已知函数y=F（2x+1）的定义域为[1，3]，求函数y=F（x）的定义域．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：（1））由1≤2x+1≤3，解出即可，（2）由3≤2x+1≤7，解出即可．
解答：
解：（1）∵函数y=F（x）定义域为[1，3]，
∴1≤2x+1≤3，
∴0≤x≤1，
∴函数y=F（2x+1）的定义域为：[0，1]；
（2）∵函数y=F（2x+1）的定义域为[1，3]，
∴3≤2x+1≤7，
∴函数y=F（x）的定义域为：[3，7]．
∴1≤2x+1≤3，
∴0≤x≤1，
∴函数y=F（2x+1）的定义域为：[0，1]；
（2）∵函数y=F（2x+1）的定义域为[1，3]，
∴3≤2x+1≤7，
∴函数y=F（x）的定义域为：[3，7]．
点评：本题考查了函数的定义域的求法，求复合函数的定义域时，注意自变量的范围的变化，本题属于基础题．
练习册系列答案
相关题目
已知函数f（x）是R上的偶函数，且在（0，+∞）上单调递减，则f（a2-2a+3）与f（-2）的大小关系为（ ）
| A、f（a2-2a+3）＞f（-2） |
| B、f（a2-2a+3）＜f（-2） |
| C、f（a2-2a+3）≥f（-2） |
| D、f（a2-2a+3）≤f（-2） |
已知函数f（x）=sinx，下面结论错误的是（ ）
| A、f（x）的最小正周期是2π | ||||||||
B、f（x）在[0，
| ||||||||
C、f（x）[
| ||||||||
| D、f（x）的值域为[-1，1] |
在△ABC中，已知sin2B-sin2C-sin2A=sinAsinC，则角B的大小为（ ）
| A、150° | B、30° |
| C、120° | D、60° |
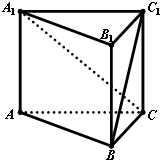在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．