题目内容
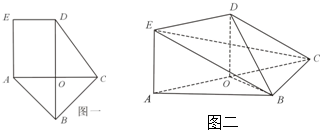
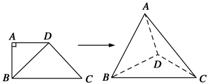如图，四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成四面体ABCD，则在四面体ABCD中，下列结论正确的是（ ）| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |
考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：由题意推出CD⊥AB，AD⊥AB，从而得到AB⊥平面ADC，又AB?平面ABC，可得平面ABC⊥平面ADC．
解答：
解：∵在四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°
∴BD⊥CD
又平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD
故CD⊥平面ABD，则CD⊥AB，又AD⊥AB
∴AB⊥平面ADC，
又AB?平面ABC，
∴平面ABC⊥平面ADC．
故选D．
∴BD⊥CD
又平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD
故CD⊥平面ABD，则CD⊥AB，又AD⊥AB
∴AB⊥平面ADC，
又AB?平面ABC，
∴平面ABC⊥平面ADC．
故选D．
点评：本题考查平面与平面垂直的判定，考查逻辑思维能力，是中档题．
练习册系列答案
相关题目
若命题甲：“p且q是真命题”，命题乙：“p或q是真命题”，则命题甲是命题乙的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
设等差数列{an}满足
=1，公差d∈（-1，0），当且仅当n=9时，数列{an}的前n项和Sn取得最大值，求该数列首项a1的取值范围（ ）
| sin2a3cos2a6-sin2a6cos2a3 |
| sin(a4+a5) |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
将长方体截去一个四棱锥，得到几何体如图所示，则该几何体的正视图为（ ）
A、 |
B、 |
C、 |
D、 |
函数y=ln（2x-1）的导数是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知关于x的不等式x2-4
xcosθ+2＜0与2x2+4xsinθ+1＜0的解集，分别是（a，b）和（
，
），且θ∈（
，π），则θ的值是（ ）
| 3 |
| 1 |
| b |
| 1 |
| a |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a∈R，则“a≥0”是“函数f（x）=x2+|x-a|在（-∞，0]上是减函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
直线L经过A（1，1），B（2，m2）两点，则直线L倾斜角的取值范围是（ ）
| A、[0°，180°） |
| B、[0°，45°） |
| C、[0°，90°）∪[135°，180°） |
| D、[135°，180°） |
