题目内容
设等差数列{an}满足
=1,公差d∈(-1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
| sin2a3cos2a6-sin2a6cos2a3 |
| sin(a4+a5) |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
考点:数列与三角函数的综合
专题:等差数列与等比数列
分析:由已知条件推导出sin(a3-a6)=1,或sin(a3+a6)=0,由仅当n=9时,数列{an}的前n项和Sn取得最大值,推导出a1=-
.由此能求出该数列首项a1的取值范围.
| 17d |
| 2 |
解答:
解:∵等差数列{an}满足
=1,
∴(sina3cosa6-sina6cosa3)(sina3cosa6+sina6cosa3)
=sin(a3+a6)=(sina3cosa6+sina6cosa3),
∴sina3cosa6-sina6cosa3=1,
即sin(a3-a6)=1,或sin(a3+a6)=0(舍)
当sin(a3-a6)=1时,
∵a3-a6=-3d∈(0,3),a3-a6=2kπ+
,k∈Z,
∴-3d=
,d=-
.
∵Sn=na1+
=
n2+(a1-
)n,
且仅当n=9时,数列{an}的前n项和Sn取得最大值,
∴-
=9,化为a1=-
.
∴a1=-
×(-
)=
.
故选:C.
| sin2a3cos2a6-sin2a6cos2a3 |
| sin(a4+a5) |
∴(sina3cosa6-sina6cosa3)(sina3cosa6+sina6cosa3)
=sin(a3+a6)=(sina3cosa6+sina6cosa3),
∴sina3cosa6-sina6cosa3=1,
即sin(a3-a6)=1,或sin(a3+a6)=0(舍)
当sin(a3-a6)=1时,
∵a3-a6=-3d∈(0,3),a3-a6=2kπ+
| π |
| 2 |
∴-3d=
| π |
| 2 |
| π |
| 6 |
∵Sn=na1+
| n(n-1)d |
| 2 |
| d |
| 2 |
| d |
| 2 |
且仅当n=9时,数列{an}的前n项和Sn取得最大值,
∴-
a1-
| ||
2×
|
| 17d |
| 2 |
∴a1=-
| 17 |
| 2 |
| π |
| 6 |
| 17π |
| 12 |
故选:C.
点评:本题综合考查了等差数列的通项公式及其性质、三角函数的平方关系和倍角公式、特殊角的三角函数等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
某学校高二年级学生有30个班,每个班的56名同学都是从1到56编的号码,为了交流学习经验,要求每班号码为16的同学留下进行交流,这里运用的是( )
| A、分层抽样 | B、抽签抽样 |
| C、随机抽样 | D、系统抽样 |
已知数列{cn}的通项是cn=
,则数列{cn}中的正整数项有( )项.
| 4n+31 |
| 2n-1 |
| A、1 | B、2 | C、3 | D、4 |
若i为虚数单位,则复数
等于( )
| i | ||
|
A、-
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
sin(-
)的值为( )
| 25π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若(1+2x)5+(a+2x)5=a1x+a2x2+a3x3+a4x4+a5x5,则a+a1+a3+a5=( )
| A、0 | B、-1 | C、243 | D、244 |
设随机变量X~B(2,P),随机变量Y~B(3,P),若P(X≥1)=
,则P(Y≥1)等于( )
| 5 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
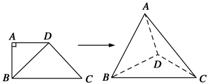 如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )
如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |