题目内容
直线L经过A（1，1），B（2，m2）两点，则直线L倾斜角的取值范围是（ ）
| A、[0°，180°） |
| B、[0°，45°） |
| C、[0°，90°）∪[135°，180°） |
| D、[135°，180°） |
考点：直线的倾斜角
专题：直线与圆
分析：求出直线的斜率，然后求出斜率的范围，即可求解倾斜角的范围．
解答：
解：直线L经过A（1，1），B（2，m2）两点，
直线的斜率为：
=m2-1≥-1．
直线的倾斜角为α，∴tanα≥-1，α∈[0°，180°）
∴α∈[0°，90°）∪[135°，180°）．
故选：C．
直线的斜率为：
| m2-1 |
| 2-1 |
直线的倾斜角为α，∴tanα≥-1，α∈[0°，180°）
∴α∈[0°，90°）∪[135°，180°）．
故选：C．
点评：本题考查直线的斜率与直线的倾斜角的关系，考查计算能力．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
若i为虚数单位，则复数
等于（ ）
| i | ||
|
A、-
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
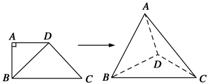如图，四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成四面体ABCD，则在四面体ABCD中，下列结论正确的是（ ）| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |
集合A={0，1，2，3，4}，B={x|x＜2}，则A∩B=（ ）
| A、∅ |
| B、{0，1} |
| C、{0，1，2} |
| D、{x|x＜2} |
在等比数列{an}中，若a1a2a3=-8，则a2等于（ ）
A、-
| ||
| B、-2 | ||
C、±
| ||
| D、±2 |
若曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”，下列方程：
①x2-y2=1
②x2-|x-1|-y=0
③xcosx-y=0
④|x|-
+1=0
其中所对应的曲线中存在“自公切线”的有（ ）
①x2-y2=1
②x2-|x-1|-y=0
③xcosx-y=0
④|x|-
| 4-y2 |
其中所对应的曲线中存在“自公切线”的有（ ）
| A、①② | B、②③ | C、①④ | D、③④ |
如图，四棱锥P-ABCD中，侧面PAD为等边三角形，AB∥CD，AB=2CD，BC⊥CD，∠DBC=30°，点E，F分别为AD，PB中点．