题目内容
已知关于x的不等式x2-4
xcosθ+2<0与2x2+4xsinθ+1<0的解集,分别是(a,b)和(
,
),且θ∈(
,π),则θ的值是( )
| 3 |
| 1 |
| b |
| 1 |
| a |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:其他不等式的解法
专题:不等式的解法及应用
分析:由题意利用韦达定理可得a+b=4
cosθ,ab=2,且
+
=-2sinθ,
=
.由此求得tanθ的值,再结合θ的范围,求得θ的值.
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
| 1 |
| 2 |
解答:
解:由题意可得a+b=4
cosθ,ab=2,且
+
=-2sinθ,
=
.
∴
=-2sinθ,
cosθ+sinθ=0,∴tanθ=-
.
再结合θ∈(
,π),可得θ=
,
故选:B.
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
| 1 |
| 2 |
∴
4
| ||
| 2 |
| 3 |
| 3 |
再结合θ∈(
| π |
| 2 |
| 2π |
| 3 |
故选:B.
点评:本题主要考查韦达定理的应用,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
sin
的值是( )
| 10π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
若(1+2x)5+(a+2x)5=a1x+a2x2+a3x3+a4x4+a5x5,则a+a1+a3+a5=( )
| A、0 | B、-1 | C、243 | D、244 |
桌上放着红桃、黑桃和梅花三种牌,共20张,下列判断正确的是( )
①桌上至少有一种花色的牌少于6张;
②桌上至少有一种花色的牌多于6张;
③桌上任意两种牌的总数将不超过19张.
①桌上至少有一种花色的牌少于6张;
②桌上至少有一种花色的牌多于6张;
③桌上任意两种牌的总数将不超过19张.
| A、①② | B、①③ | C、②③ | D、①②③ |
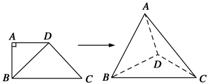 如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )
如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |
集合A={0,1,2,3,4},B={x|x<2},则A∩B=( )
| A、∅ |
| B、{0,1} |
| C、{0,1,2} |
| D、{x|x<2} |