题目内容
在等差数列{an}中,若a3+a11=10,则a7= .
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:在等差数列{an}中,
∵a3+a11=2a7=10,
∴a7=5.
故答案为:5.
∵a3+a11=2a7=10,
∴a7=5.
故答案为:5.
点评:本题考查数列的第7项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
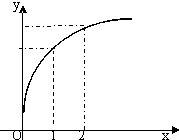
函数f(x)的图象如图所示,下列数值排序正确的是( )

| A、0<f′(1)<f′(2)<f(2)-f(1) |
| B、0<f′(2)<f(2)-f(1)<f′(1) |
| C、0<f′(2)<f′(1)<f(2)-f(1) |
| D、0<f(2)-f(1)<f′(1)<f′(2) |
关于x的方程x2+(m-2)x+5-m=0的两根均大于2,则实数m的取值范围是( )
| A、(-5,-4] |
| B、(-∞,-5)∪(-5,-4) |
| C、(-∞,-4] |
| D、(-∞,-2) |
已知数列{an}满足a1=4,an=4-
(n≥2),则a6=( )
| 4 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
