题目内容
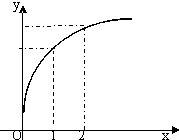
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
| A、0＜f′（1）＜f′（2）＜f（2）-f（1） |
| B、0＜f′（2）＜f（2）-f（1）＜f′（1） |
| C、0＜f′（2）＜f′（1）＜f（2）-f（1） |
| D、0＜f（2）-f（1）＜f′（1）＜f′（2） |
考点：利用导数研究函数的单调性,函数的图象
专题：导数的综合应用
分析：由题意已知函数f（x）的图象，先判断它的单调性，然后根据函数图象斜率的变化，判断f（x）′的增减性，最后根据函数的凸凹性进行判断，从而求解．
解答：
解：由函数f（x）的图象可知：
当x≥0时，f（x）单调递增，且当x=0时，f（0）＞0，
∴f′（2），f′（1），f（2）-f（1）＞0，
由此可知f（x）′在（0，+∝）上恒大于0，其图象为一条直线，
∵直线的斜率逐渐减小，
∴f′（x）单调递减，
∴f′（1）＞f′（2），
∵f（x）为凸函数，
∴f（2）-f（1）＜f′（1）
∴0＜f′（2）＜f（2）-f（1）＜f′（1），
故选B
当x≥0时，f（x）单调递增，且当x=0时，f（0）＞0，
∴f′（2），f′（1），f（2）-f（1）＞0，
由此可知f（x）′在（0，+∝）上恒大于0，其图象为一条直线，
∵直线的斜率逐渐减小，
∴f′（x）单调递减，
∴f′（1）＞f′（2），
∵f（x）为凸函数，
∴f（2）-f（1）＜f′（1）
∴0＜f′（2）＜f（2）-f（1）＜f′（1），
故选B
点评：本题主要考查函数导数与函数单调性之间的关系，掌握并会熟练运用导数与函数单调性的关系，另外还考查学生的读图能力，要善于从图中获取信息．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
北京奥运吉祥物由5个不同的“福娃”组成，将它们在展示台上随意摆放成一列，则不同的摆放顺序有（ ）
| A、1种 | B、5种 |
| C、60种 | D、120种 |
已知0＜a＜1，b＞1且ab＞1，则下列不等式成立的是（ ）
A、logb
| ||||
B、logab＜logb
| ||||
C、logab＜loga
| ||||
D、logb
|
已知直线y=kx+2和椭圆2x2+3y2=6有两个公共点，则k的取值范围（ ）
A、k＜-
| ||||||||
B、-
| ||||||||
C、k≤-
| ||||||||
D、-
|