题目内容
3.若方程$\frac{{x}^{2}}{10-k}$+$\frac{{y}^{2}}{5-k}$=1表示双曲线,则k的取值范围是( )| A. | (5,10) | B. | (-∞,5) | C. | (10,+∞) | D. | (-∞,5)∪(10,+∞) |
分析 根据题意,由双曲线的标准方程的形式分析可得(10-k)与(5-k)异号,即可得(10-k)(5-k)<0,解可得k的范围,即可得答案.
解答 解:根据题意,方程$\frac{{x}^{2}}{10-k}$+$\frac{{y}^{2}}{5-k}$=1表示双曲线,
必有(10-k)与(5-k)异号,
即有(10-k)(5-k)<0,
解可得5<k<10,
即k的取值范围是(5,10);
故选:A.
点评 本题考查双曲线的标准方程,关键是注意双曲线标准方程的形式,即二元二次方程在什么条件下表示双曲线.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
13.下面各组函数中为相同函数的是( )
| A. | $f(x)=\sqrt{{{(x-1)}^2}},g(x)=x-1$ | B. | f(x)=x0,g(x)=1 | ||
| C. | $f(x)={3^x},g(x)={(\frac{1}{3})^{-x}}$ | D. | $f(x)=x-1,g(x)=\frac{{{x^2}-1}}{x+1}$ |
6.下列函数中,既是奇函数又在区间(0.+∞)上单调递增的函数是( )
| A. | y=1nx | B. | y=x3 | C. | y=2|x | | D. | y=-x |
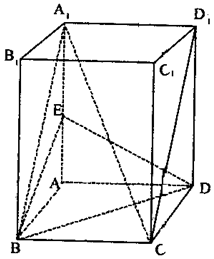 如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.
如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.