题目内容

已知函数f（x）=
1
2
ax2-lnx+1，试讨论此函数的单调性．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，通过讨论a的取值范围求出函数的单调区间．
解答： 解：∵f′（x）=ax-
1
x
=
ax2-1
x
（x＞0），
a≤0时，f′（x）＜0，f（x）的单调递减区间为：（0，+∞），
a＞0时，f（x）在（0，
a
a
）递减，在（
a
a
，+∞）递增．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
已知函数f（x）=lnx-
a(x-1)
x+1

（Ⅰ）若函数f（x）在（0，+∞）上为单调递增函数，求实数a的取值范围；
（Ⅱ）设m＞n＞0，求证：
lnm-lnn
2
＞
m-n
m+n
．
已知角α的终边经过点P（-3，-
3
）．
（Ⅰ）求sinα、cosα、tanα的值；
（Ⅱ）求
1+sinα
1-sinα
-
1-sinα
1+sinα
的值．
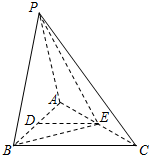如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．
（1）求证：DE∥平面PBC；
（2）求证：AB⊥PE．
已知向量
m
=（cosωx，1），
n
=（
3
，sinωx）（ω＞0），函数f（x）=
m
•
n
，且f（x）图象上一个最高点为P（
π
12
，2），与P最近的一个最低点的坐标为（
7π
12
，-2）．
（1）求函数f（x）的解析式；
（2）设a为常数，判断方程f（x）=a在区间[0，
π
2
]上的解的个数；
（3）在锐角△ABC中，若cos（
π
3
-B）=1，求f（A）的取值范围．
数列{an}的前n项和记作Sn，满足 Sn=2an+3n-12（n∈N*）
（Ⅰ）证明数列{an-3}为等比数列，并求出数列{an}的通项公式；
（Ⅱ）记bn=nan，数列{bn}的前n项和为Tn，求Tn．
设数列{an}的前n项和为Sn，已知Sn=2an-2n+1（n∈N*）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：当x＞0时，ln(x+1)＞
x
x+1
；
（Ⅲ）令cn=(-1)n+1log
an
n+1
2，数列{cn}的前2n项和为T2n．利用（2）的结论证明：当n∈N*且n≥2时，
T
 
2n
＜ln2．
将演绎推理：“y=log
1
2
x在（0，+∞）上是减函数”恢复成完全的三段论，其中大前提是
 
．
若实数a，b，c，d满足ab=2，c+2d=0，则（a-c）2+（b-d）2的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网