题目内容
圆
(θ为参数)与直线3x-4y-9=0的位置关系是( )
|
| A、相切 | B、相离 |
| C、直线过圆心 | D、相交但直线不过圆心 |
考点:圆的参数方程
专题:坐标系和参数方程
分析:把参数方程化为直角坐标方程,求出圆心和半径,根据圆心到直线3x-4y-9=0的距离小于半径,可得直线和圆相交.再根据圆心的坐标不满足直线方程,可得直线不过圆心,从而得出结论.
解答:
解:把圆
(θ为参数),消去参数,化为直角坐标方程为 x2+y2=4,
表示以原点为圆心、半径等于2的圆.
圆心到直线3x-4y-9=0的距离为d=
=
<2,故直线和圆相交.
再根据圆心的坐标不满足直线方程,可得直线不过圆心,
故选:D.
|
表示以原点为圆心、半径等于2的圆.
圆心到直线3x-4y-9=0的距离为d=
| |0-0-9| | ||
|
| 9 |
| 5 |
再根据圆心的坐标不满足直线方程,可得直线不过圆心,
故选:D.
点评:本题主要考查把参数方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
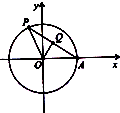 如图,A是单位圆与x轴正半轴的交点,点P在该单位圆上,∠AOP=θ(0<θ<π),点Q满足
如图,A是单位圆与x轴正半轴的交点,点P在该单位圆上,∠AOP=θ(0<θ<π),点Q满足| PQ |
| QA |
| OA |
| OQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
定积分
(
-x)dx等于( )
| ∫ | 1 0 |
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某算法的程序框如图所示,若输出结果为
,则输入的实数x的值是( )

| 1 |
| 2 |

A、-
| ||
B、
| ||
C、
| ||
| D、4 |
已知向量
=(1,2),
=(-2,t),
∥
,则t=( )
| m |
| n |
| m |
| n |
| A、-4 | B、-2 | C、0 | D、1 |
若102x=25,则x=( )
A、lg
| ||
| B、lg5 | ||
| C、2lg5 | ||
D、2lg
|
已知等边三角形的边长为4,那么它水平放置的直观图的面积为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
若抛物线y2=4x的焦点是F,准线是l,则经过点F、M(4,4)且与l相切的圆共有( )
| A、4个 | B、2个 | C、1个 | D、0个 |