题目内容
17.已知双曲线Γ1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,椭圆Γ2:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{6}$=1的离心率为e,直线MN过F2与双曲线交于M,N两点,若cos∠F1MN=cos∠F1F2M,$\frac{|{F}_{1}M|}{|{F}_{1}N|}$=e,则双曲线Γ1的两条渐近线的倾斜角分别为( )| A. | 30°或150° | B. | 45°或135° | C. | 60°或120° | D. | 15°或165° |
分析 用a,b,c表示出MF1,MF2,NF1,NF2,利用余弦定理计算cos∠F1F2M和cos∠F1F2N,由∠F1F2M+∠F1F2N=0计算出离心率e1,得出a和b的关系即可得出答案.
解答  解:∵cos∠F1MN=cos∠F1F2M,
解:∵cos∠F1MN=cos∠F1F2M,
∴∠F1MN=∠F1F2M,
∴|MF1|=|F1F2|=2c,
由双曲线的定义可得|MF2|=|MF1|-2a=2c-2a,
∵椭圆Γ2:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{6}$=1的离心率为e=$\frac{\sqrt{8-6}}{\sqrt{8}}$=$\frac{1}{2}$,
∴$\frac{|{F}_{1}M|}{|{F}_{1}N|}$=$\frac{1}{2}$,∴|NF1|=4c,|NF2|=4c-2a,
在△MF1F2中,由余弦定理的
cos∠F1F2M=$\frac{4{c}^{2}+(2c-2a)^{2}-4{c}^{2}}{2×2c×(2c-2a)}$=$\frac{c-a}{2c}$,
在△NF1F2中,由余弦定理的cos∠F1F2N=$\frac{4{c}^{2}+(4c-2a)^{2}-16{c}^{2}}{2×2c×(4c-2a)}$=$\frac{{a}^{2}+{c}^{2}-4ac}{2c(2c-a)}$,
∵∠F1F2M+∠F1F2N=π,
∴cos∠F1F2M+cos∠F1F2N=0,即$\frac{c-a}{2c}$+$\frac{{a}^{2}+{c}^{2}-4ac}{2c(2c-a)}$=0,
整理得2a2+3c2-7ac=0,设双曲线的离心率为e1,
∴3e12-7e1+2=0,解得e1=2或$\frac{1}{3}$(舍).
∴$\frac{{a}^{2}+{b}^{2}}{{a}^{2}}$=4,∴3a2=b2,即$\frac{b}{a}$=$\sqrt{3}$.
∴双曲线的渐近线方程为y=±$\sqrt{3}$x,
∴渐近线的倾斜角为60°和120°.
故选C.
点评 本题考查了双曲线的定义,离心率计算,余弦定理,属于中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下认为40岁以上的人患胃病与否和生活规律有关系吗?为什么?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 男 | 女 | |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为泰华中学的高二学生选报文理科与性别有关?
注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| A. | $\frac{1}{{3•{2^{n-1}}}}$ | B. | $\frac{1}{{2•{3^{n-1}}}}$ | C. | $\frac{1}{2^n}$ | D. | $\frac{n}{3^n}$ |
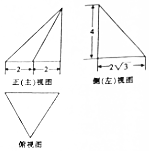
| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | 8 | B. | 9 | C. | 2 | D. | 6$\sqrt{6}$ |