题目内容
将函数y=sin（2x+φ）（|φ|≤
）的图象向左平移
个单位后，得到一个偶函数的图象，则φ的一个可能值等于 ．
| π |
| 2 |
| π |
| 6 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件根据函数y=Asin（ωx+φ）的图象变换规律，正弦函数、余弦函数的图象的对称性，可得
+φ=kπ+
，k∈z，由此求得φ的一个可能值．
| π |
| 3 |
| π |
| 2 |
解答：
解：将函数y=sin（2x+φ）（|φ|≤
）的图象向左平移
个单位后，
得到函数y=sin[2（x+
）+φ）]=sin（2x+
+φ）的图象，
再根据所得函数为偶函数，可得
+φ=kπ+
，k∈z，即φ=kπ+
，
则φ的一个可能值等于
，
故答案为：
．
| π |
| 2 |
| π |
| 6 |
得到函数y=sin[2（x+
| π |
| 6 |
| π |
| 3 |
再根据所得函数为偶函数，可得
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
则φ的一个可能值等于
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数、余弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
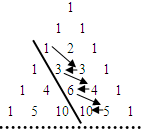如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10…，记其前n项和为Sn，则S41的值为