题目内容

已知函数f（x）=
2x+1
2x-1

（1）求f（x）的定义域；
（2）判断f（x）的奇偶性．
考点：函数奇偶性的判断,函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：（1）由2x-1≠0得：x≠0，从而可得f（x）的定义域；
（2）利用f（-x）+f（x）=0即可判断其奇偶性．
解答： 解：（1）由2x-1≠0得：x≠0，
∴f（x）的定义域为{x|x≠0}；
（2）∵f（-x）+f（x）=
2-x+1
2-x-1
+
2x+1
2x-1
=
1+2x
1-2x
+
2x+1
2x-1
=0，
∴f（-x）=-f（x），
∴函数f（x）=
2x+1
2x-1
为奇函数．
点评：本题考查函数奇偶性的判断，考查函数的定义域及其求法，属于中档题．
练习册系列答案
相关题目
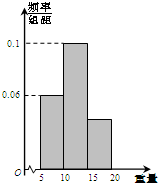如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为（　　）
A、10B、20C、30D、40
（用分析法或者综合法证明）已知a＞6，求证：
a-3
-
a-4
＜
a-5
-
a-6
．
已知函数f（x）=ax2+bx+1有相异零点x1，x2（x1＜x2），函数g（x）=a2x2+bx+1有相异零点x3，x4（x3＜x4），若a＞1，求证：x1＜x3＜x4＜x2．
（1）若对一切实数x，不等式|x-3|-|x+2|＞a恒成立，求实数a的取值范围；
（2）若不等式|x-3|-|x+2|＞a有解，求实数a的取值范围；
（3）若方程|x-3|-|x+2|=a有解，求实数a的取值范围．
以椭圆
x2
25
+
y2
9
=1焦点为顶点，离心率为2的双曲线方程为
 
．
设[x]表示不超过x的最大整数，如：[1]=1，[1.3]=1，[-1.5]=-2，给出下列命题：
①若函数f（x）=[x]-x，则有f（x+1）=f（x）；
②若函数f（x）=[x]-x，则f（x）的值域为（-1，0]；
③当x∈[0，π]时，方程[2sinx]=|
2
|的解集为[
π
6
，
5π
6
]；
④当x∈[0，n）（n∈N+）时，设函数g（x）=[x]的值域为An，记An中的元素个数为an，则数列{an}的前n项和Sn=
n(n+1)
2
．
其中正确的命题的序号是
 
．
已知集合S={x|-1≤x≤4}，若非空集合T满足条件：（S∩T）?（S∪T），则集合T等于
 
．
设集合M={x|y2=3x，x∈R}，N={y|x2+y2=4，x∈R，y∈R}，则M∩N等于（　　）
A、{
3
，-
3
}
B、[-2，2]
C、{(1，
3
)，(1，-
3
)}
D、[0，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网