题目内容
设a∈R,若对任意的n∈N*时,不等式(an-20)ln(
)≥0恒成立,则a的取值范围是( )
| n |
| a |
| A、(-∞,5] |
| B、[4,5] |
| C、(4,5) |
| D、[1,5] |
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式进行等价转化,然后分离出参数t后化为函数的最值可求,注意n的取值范围.
解答:
解不等式(an-20)ln(
)≥0恒成立等价为
或
,
即
或
,
∴
①或
②,
对于①有n≥5,
∵对于n恒成立,
∴t≥(
)max=4,且t≤nmin=5,
∴t∈[4,5];
同理由②也得t∈[4,5],
综上得,t∈[4,5].
故选:B.
| n |
| a |
|
|
即
|
|
∴
|
|
对于①有n≥5,
∵对于n恒成立,
∴t≥(
| 20 |
| n |
∴t∈[4,5];
同理由②也得t∈[4,5],
综上得,t∈[4,5].
故选:B.
点评:本题考查函数恒成立问题,不等式的等价转化,考查转化思想,准确理解题意是解决该题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
若在数列{an}中,对任意正整数n,都有
+
=p(常数),则称数列{an}为“等方和数列”,称p为“公方和”,若数列{an}为“等方和数列”,其前n项和为Sn,且“公方和”为1,首项a1=1,则S2014的最大值与最小值之和为( )
| a | 2 n |
| a | 2 n+1 |
| A、2014 | B、1007 |
| C、-1 | D、2 |
对?x∈R,函数f(x)=x2+bx+c的值恒非负,若b>3,则
的最小值为( )
| 1+b+c |
| b-3 |
| A、3 | B、4 | C、5 | D、7 |
已知锐角△ABC中,|
|=4,|
|=1,△ABC的面积为
,则
•
的值为( )
| AB |
| AC |
| 3 |
| AB |
| AC |
| A、-2 | B、2 | C、4 | D、-4 |
若对一切x∈R,mx2+2mx-3<0恒成立,则实数m的取值范围为( )
| A、(-3,0) |
| B、(-3,0] |
| C、(-∞,-3] |
| D、(-∞,0] |
已知函数f(x)=mx3+3(m-1)x2-m2+1(m>0)的单调递减区间是(0,4),则m=( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
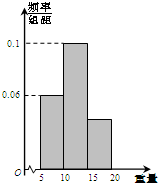 如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )
如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )