题目内容
已知圆C：
（θ为参数），与x轴交与A、B两点，则|AB|等于（ ）
|
| A、6 | B、4 | C、2 | D、0 |
考点：圆的参数方程
专题：坐标系和参数方程
分析：把圆C：
（θ为参数）的方程消去参数化为普通方程，在圆的方程中，令y=0求得x的值，可得
|AB|的值．
|
|AB|的值．
解答：
解：把圆C：
（θ为参数）的方程消去参数化为普通方程为 （x+3）2+y2=4．
在圆的方程中，令y=0可得x=-1，或 x=-5，故|AB|=|-1-（-5）|=4，
故选：B．
|
在圆的方程中，令y=0可得x=-1，或 x=-5，故|AB|=|-1-（-5）|=4，
故选：B．
点评：本题主要考查把参数方程化为普通方程的方法，直线和圆的位置关系，属于中档题．
练习册系列答案
相关题目
已知锐角△ABC中，|
|=4，|
|=1，△ABC的面积为
，则
•
的值为（ ）
| AB |
| AC |
| 3 |
| AB |
| AC |
| A、-2 | B、2 | C、4 | D、-4 |
向量
=（3，-4），向量|
|=2，若
•
=-5，那么向量
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数 f(x)=
．若对任意的实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，则实数k的取值范围是（ ）
| 4x+k•2x+1 |
| 4x+2x+1 |
| A、0＜k≤3 | ||
| B、1≤k≤4 | ||
C、-
| ||
D、-
|
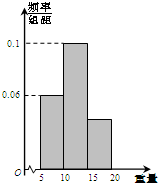如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为（ ）