题目内容
已知抛物线y2=4x的准线过双曲线
-
=1(a>0,b>0)的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
A、
| ||
| B、4 | ||
| C、3 | ||
| D、2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线y2=4x的准线方程,可得双曲线
-
=1(a>0,b>0)的左焦点,求出x=-1时,y的值,利用△AOB的面积为
,求出a,即可求双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
解答:
解:∵抛物线y2=4x的准线方程为x=-1,
∴双曲线
-
=1(a>0,b>0)的左焦点为(-1,0)
x=-1时,代入双曲线方程,由b2=1-a2,可得y=±
,
∵△AOB的面积为
,
∴
•1•
=
,
∴a=
,
∴e=
=2.
故选:D.
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
x=-1时,代入双曲线方程,由b2=1-a2,可得y=±
| 1-a2 |
| a |
∵△AOB的面积为
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 2(1-a2) |
| a |
| 3 |
| 2 |
∴a=
| 1 |
| 2 |
∴e=
| c |
| a |
故选:D.
点评:本题考查抛物线、双曲线的几何性质,考查三角形面积的计算,正确运用抛物线、双曲线的几何性质是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
若在数列{an}中,对任意正整数n,都有
+
=p(常数),则称数列{an}为“等方和数列”,称p为“公方和”,若数列{an}为“等方和数列”,其前n项和为Sn,且“公方和”为1,首项a1=1,则S2014的最大值与最小值之和为( )
| a | 2 n |
| a | 2 n+1 |
| A、2014 | B、1007 |
| C、-1 | D、2 |
已知函数f(x)=mx3+3(m-1)x2-m2+1(m>0)的单调递减区间是(0,4),则m=( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
向量
=(3,-4),向量|
|=2,若
•
=-5,那么向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数 f(x)=
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是( )
| 4x+k•2x+1 |
| 4x+2x+1 |
| A、0<k≤3 | ||
| B、1≤k≤4 | ||
C、-
| ||
D、-
|
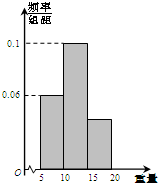 如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )
如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为( )