题目内容
3.在△ABC中,角A,B,C所对的边分别为a,b,c,已知$\frac{{sin({A+B})}}{a+b}=\frac{sinA-sinB}{a-c}$,b=3.(Ⅰ)求角B;
(Ⅱ)若$cosA=\frac{{\sqrt{6}}}{3}$,求△ABC的面积.
分析 (Ⅰ)由三角形内角和定理,正弦定理化简已知等式得a2+c2-b2=ac,由余弦定理cosB的值,结合范围B∈(0,π),可求B的值.
(Ⅱ)利用同角三角函数基本关系式可求sinA,由正弦定理可得a的值,利用两角和的正弦函数公式可求sinC的值,进而利用三角形面积公式即可计算得解.
解答 (本题满分为12分)
解:(Ⅰ)因为A+B+C=π,
所以A+B=π-C,…(1分)
所以sin(A+B)=sinC,…(2分)
由正弦定理得:$\frac{c}{a+b}=\frac{a-b}{a-c}$,…(3分)
整理得a2+c2-b2=ac,…(4分)
由余弦定理得:$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{ac}{2ac}=\frac{1}{2}$. …(5分)
又B∈(0,π),
所以$B=\frac{π}{3}$. …(6分)
(Ⅱ)因为$cosA=\frac{{\sqrt{6}}}{3}$,且A∈(0,π),
所以sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{3}}{3}$,…7分
由正弦定理可得:$\frac{a}{\frac{\sqrt{3}}{3}}$=$\frac{3}{\frac{\sqrt{3}}{2}}$,
解得a=2. …(8分)
又sinC=sin(A+B)=sinAcosB+cosAsinB…(9分)
=$\frac{{\sqrt{3}}}{3}×\frac{1}{2}+\frac{{\sqrt{6}}}{3}×\frac{{\sqrt{3}}}{2}$=$\frac{{\sqrt{3}+3\sqrt{2}}}{6}$. …(10分)
所以△ABC的面积$S=\frac{1}{2}absinC$=$\frac{1}{2}×2×3×\frac{{\sqrt{3}+3\sqrt{2}}}{6}$…(11分)
=$\frac{{\sqrt{3}+3\sqrt{2}}}{6}$. …(12分)
点评 本题主要考查了三角形内角和定理,正弦定理,余弦定理,同角三角函数基本关系式,两角和的正弦函数公式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | y2=2x | B. | y2=4x | C. | y2=6x | D. | y2=8x |
| A. | “$sinθ=\frac{1}{2}$”是“θ=30°”的充分不必要条件 | |
| B. | 命题p:?n0∈N,${2^{n_0}}>1000$,则¬p:?n∈N,2n≤1000 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| D. | 命题“若?x∈(0,+∞),则2x<3x”是真命题 |
| A. | f(x)=cos(2x$+\frac{π}{3}$) | B. | f(x)=-cos(2x-$\frac{π}{6}$) | C. | f(x)=-sin(2x+$\frac{π}{6}$) | D. | f(x)=sin(2x-$\frac{π}{6}$) |
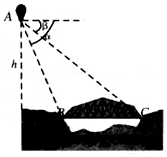 如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.
如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.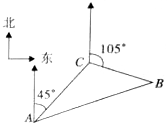 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.