题目内容
14．
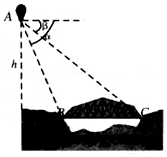如图，从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°，β=45°，如果此时气球的高度h是10米，则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米．
分析 由题意画出图形，通过求解两个直角三角形得到DC和DB的长度，作差后可得答案．
解答 解：如图，设过A作BC的垂线，垂足为D，则∠DAB=30°，
∴BD=$\frac{10\sqrt{3}}{3}$．
在Rt△ADC中，又AD=10，∠DAC=45°，∴DC=10，
∴BC=DC-DB=10-$\frac{10\sqrt{3}}{3}$（m）．
∴河流的宽度BC等于（10-$\frac{10\sqrt{3}}{3}$）m．
故答案为10-$\frac{10\sqrt{3}}{3}$．
点评 本题给出实际应用问题，求河流在B、C两地的宽度，着重考查了三角函数的定义，属于中档题．
练习册系列答案
相关题目
5．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为2$\sqrt{5}$，且双曲线的一条渐近线与直线2x+y=0垂直，则双曲线的顶点到渐近线的距离为（ ）
| A． | 1 | B． | 2 | C． | $\frac{2\sqrt{5}}{5}$ | D． | $\frac{4\sqrt{5}}{5}$ |
2．若实数x，y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$，则$\frac{y}{1-x}$的取值范围为（ ）
| A． | $（{-∞，-\frac{4}{3}}]$ | B． | $（{-∞，\frac{3}{4}}）$ | C． | $[{-\frac{3}{4}，+∞}）$ | D． | $[{-\frac{4}{3}，+∞}）$ |
19．已知实数x，y满足约束条件$\left\{\begin{array}{l}{|x-2y+2|≤2}\\{|x+3y-8|≤2}\end{array}\right.$，则z=x+2y的最大值为（ ）
| A． | 4 | B． | 8 | C． | $\frac{24}{5}$ | D． | $\frac{36}{5}$ |