题目内容
11.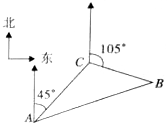 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
分析 设所需时间为t小时,在点B处相遇则可求得AB和BC,进而利用余弦定理建立等式求得t.
解答 解:设所需时间为t小时,在点B处相遇在△ABC中,
∠ACB=120°,AC=100,AB=21t,BC=9t,由余弦定理:
(21t)2=102+(9t)2-2×10×9t×cos120°
整理得:36t2-9t-10=0
解得:t=$\frac{2}{3}$或-$\frac{5}{12}$(舍负)
故救生艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 本题主要考查了解三角形的实际应用.解题的关键是利用了余弦定理,利用已知的边和角建立方程求得时间.

练习册系列答案
相关题目
2.若实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$,则$\frac{y}{1-x}$的取值范围为( )
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
19.已知实数x,y满足约束条件$\left\{\begin{array}{l}{|x-2y+2|≤2}\\{|x+3y-8|≤2}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | 4 | B. | 8 | C. | $\frac{24}{5}$ | D. | $\frac{36}{5}$ |
20.i为虚数单位,复数$\frac{2i}{1-i}$在复平面内对应的点到原点的距离为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
1.函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{\frac{1}{16}{x}^{2}(0≤x≤2)}\\{(\frac{1}{2})^{x}(x>2)}\end{array}\right.$,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有5个不同实数根,则实数a的取值范围是( )
| A. | (-$\frac{1}{4}$,0) | B. | ($-\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($-\frac{1}{2}$,$-\frac{1}{4}$)∪($-\frac{1}{4}$,-$\frac{1}{8}$) | D. | (-$\frac{1}{2}$,$-\frac{1}{8}$) |
 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.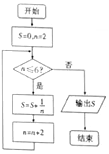 如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.
如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.