题目内容
8.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且$\frac{c}{b}=\sqrt{2}sinC$.(1)求B;
(2)若a=6,△ABC的面积为9,求b的长,并判断△ABC的形状.
分析 (1)由已知及正弦定理可得sinB=$\frac{\sqrt{2}}{2}$,结合范围0<B<π,可得B的值.
(2)利用三角形面积公式可求c,进而利用余弦定理可求b的值,分类讨论,即可判定三角形的形状.
解答 解:(1)由$c=\sqrt{2}bsinC$,可得$\frac{c}{sinC}=\frac{b}{{\frac{{\sqrt{2}}}{2}}}$.
根据正弦定理可得:sinB=$\frac{\sqrt{2}}{2}$,
由于0<B<π,可得:B=$\frac{π}{4}$或$\frac{3π}{4}$,
(2)因为△ABC的面积为9=$\frac{1}{2}$acsinB,a=6,sinB=$\frac{\sqrt{2}}{2}$,
所以$\frac{1}{2}×6c×\frac{{\sqrt{2}}}{2}=9$.
解得$c=3\sqrt{2}$.
由余弦定理可知${b^2}={a^2}+{c^2}-2accosB=54-36\sqrt{2}cosB$,
由$cosB=±\frac{{\sqrt{2}}}{2}$得b2=18或b2=90,
所以$b=3\sqrt{2}$或$b=3\sqrt{10}$.
当$b=3\sqrt{2}$时,此时$b=c=3\sqrt{2},a=6$,△ABC为等腰直角三角形;
当$b=3\sqrt{10}$时,此时$c=3\sqrt{2},a=6$,△ABC为钝角三角形.
点评 本题主要考查了正弦定理,三角形面积公式,余弦定理在解三角形中的应用,考查了转化思想和分类讨论思想,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.表面积为3π的圆锥的侧面展开图是一个半圆,则该圆锥的底面圆半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.已知实数x,y满足约束条件$\left\{\begin{array}{l}{|x-2y+2|≤2}\\{|x+3y-8|≤2}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | 4 | B. | 8 | C. | $\frac{24}{5}$ | D. | $\frac{36}{5}$ |
13.已知△ABC的三边长a,b,c成递减的等差数列,若$B=\frac{π}{4}$,则cosA-cosC=( )
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\root{4}{2}$ | D. | $\root{4}{2}$ |
20.i为虚数单位,复数$\frac{2i}{1-i}$在复平面内对应的点到原点的距离为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
17.已知数列{an}的通项公式为an=$\frac{1}{n(n+2)}$,前n项和为Sn,若实数λ满足(-1)nλ<3+(-1)n+1Sn对任意正整数n恒成立,则实数λ的取值范围是( )
| A. | $-\frac{10}{3}$<λ≤$\frac{9}{4}$ | B. | $-\frac{10}{3}$<λ<$\frac{9}{4}$ | C. | $-\frac{9}{4}$<λ≤$\frac{10}{3}$ | D. | $-\frac{9}{4}$<λ<$\frac{10}{3}$ |
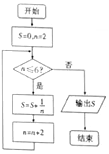 如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.
如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.