题目内容
13.若抛物线y2=2px(p>0)上一点P(2,y0)到其准线的距离为4,则抛物线的标准方程为( )| A. | y2=2x | B. | y2=4x | C. | y2=6x | D. | y2=8x |
分析 利用抛物线的简单性质,转化求解p,即可得到抛物线方程.
解答 解:抛物线y2=2px(p>0)上一点P(2,y0)到其准线的距离为4,
可得$\frac{p}{2}$+2=4,解得p=4,
则抛物线的标准方程为y2=8x.
故选:D.
点评 本题考查抛物线的简单性质以及抛物线方程的求法,考查计算能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
18.表面积为3π的圆锥的侧面展开图是一个半圆,则该圆锥的底面圆半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2$\sqrt{5}$,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的顶点到渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
2.若实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$,则$\frac{y}{1-x}$的取值范围为( )
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
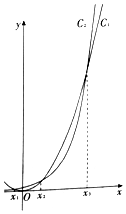 函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点.
函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点. 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.