题目内容
已知函数f（x+1）=x2-2x+1的定义域为[-2，0]，则函数f（x）的最大值为 ．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：首先求出函数的解析式，然后求二次函数的最值．
解答：
解：因为f（x+1）=x2-2x+1=（x+1）2-4（x+1）+4，
所以函数解析式为f（x）=x2-4x+4，
又因为f（x+1）=x2-2x+1的定义域为[-2，0]，所以x+1∈[-1，1]，
所以f（x）的定义域为[-1，1]，并且f（x）在[-1，1]上是减函数，
所以f（x）的最大值为f（-1）=1+4+4=9；
故答案为：9．
所以函数解析式为f（x）=x2-4x+4，
又因为f（x+1）=x2-2x+1的定义域为[-2，0]，所以x+1∈[-1，1]，
所以f（x）的定义域为[-1，1]，并且f（x）在[-1，1]上是减函数，
所以f（x）的最大值为f（-1）=1+4+4=9；
故答案为：9．
点评：本题考查了复合函数的定义域求法、解析式的求法以及二次函数解析式最值求法．
练习册系列答案
相关题目
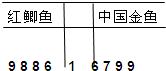已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼．为了估计池塘中这两种鱼的数量，养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只，给每只鱼作上不影响其存活的记号，然后放回池塘，经过一定时间，再每次从池塘中随机地捕出1000只鱼，分类记录下其中有记号的鱼的数目，随即将它们放回池塘中．这样的记录作了10次．并将记录获取的数据做成以下的茎叶图，已知向量
=（sinθ，-2）与
=（1，cosθ）互相垂直，其中θ∈（0，
），则
=（ ）
| a |
| b |
| π |
| 2 |
| 1 |
| sin2θ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}中，已知an=2n-17，该数列中相邻两项积为负数的是（ ）
| A、a6和a7 |
| B、a7和a8 |
| C、a8和a9 |
| D、a9和a10 |