题目内容
设定义在R上的奇函数y=f(x),满足对任意t∈R,都有f(t)=f(2-t),且x∈(0,1]时,f(x)=-x2+4x,则f(3)的值等于( )
| A、-3 | B、-55 | C、3 | D、55 |
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:由f(t)=f(2-t),且f(x)为奇函数,可得f(3)=f(2-3)=f(-1)=-f(1),
再由x∈(0,1]时,f(x)=-x2+4x,求出f(1),从而可求f(3).
再由x∈(0,1]时,f(x)=-x2+4x,求出f(1),从而可求f(3).
解答:
解:∵对任意t∈R,都有f(t)=f(2-t),且f(x)为奇函数,
∴f(3)=f(2-3)=f(-1)=-f(1),
∵x∈(0,1]时,f(x)=-x2+4x,则f(1)=-1+41=3,
∴f(3)=-f(1)=-3,
故选:A
∴f(3)=f(2-3)=f(-1)=-f(1),
∵x∈(0,1]时,f(x)=-x2+4x,则f(1)=-1+41=3,
∴f(3)=-f(1)=-3,
故选:A
点评:本题主要考查函数的性质,对于抽象函数的问题,要反复运用所给的条件来代换,属于基础题.

练习册系列答案
相关题目
在2,0,1,5这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
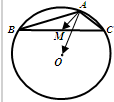 如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则
如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则| AM |
| AO |
| A、-10 | B、36 | C、16 | D、13 |
 如图,△ABC的重心为G,O是△ABC所在平面上一点,
如图,△ABC的重心为G,O是△ABC所在平面上一点,